A força eletrostática e a lei de Coulomb
Além das famosas três leis da Mecânica, Newton mostrou que a força que mantém a Terra orbitando em torno do Sol, da Lua orbitando em torno da Terra, da maça caindo próxima à superfície da Terra, todas elas tem uma mesma origem: a força gravitacional. Segundo a lei de gravitação universal de Newton, duas massas puntifomes, ![]() e
e ![]() , separadas por uma distância
, separadas por uma distância ![]() , sofrem uma atração mútua, dada por
, sofrem uma atração mútua, dada por
(1) ![]()
Na linguagem matemática ![]() é um vetor unitário (módulo igual a 1) que diz que essa força está na direção que as duas massas. O sinal negativo diz que a força em questão é atrativa.
é um vetor unitário (módulo igual a 1) que diz que essa força está na direção que as duas massas. O sinal negativo diz que a força em questão é atrativa.
![]() é a chamada constante universal da gravitação. Por “universal”, que dizer que não depende da Natureza das massas; ela é igual para todas as massas.
é a chamada constante universal da gravitação. Por “universal”, que dizer que não depende da Natureza das massas; ela é igual para todas as massas.
A força gravitacional é uma das forças fundamentais da Natureza.
Existem outras forças ditas fundamentais da Natureza? Na verdade hoje acreditamos que existem mais três: além da força gravitacional, existe a força eletromagnética, a força fraca e a força forte.
As duas últimas forças são de curtíssimo alcance e portanto são importantes somente em processos atômicos e subatômicos (por exemplo, a força fraca é responsável pelo decaimento do nêutron livre).
A força eletromagnética é uma combinação das forças elétrica e magnética. Nesta página vamos nos focar somente na força elétrica devido a cargas em repouso ou que não estejam muito aceleradas, situação em que descreveremos como um sistema estático ou estacionário.
Na situação eletrostática, a força elétrica é conhecida também como força coulombiana, em homenagem ao cientista francês Charles A. Coulomb.
A lei que leva o seu nome diz que duas cargas puntiformes, ![]() e
e ![]() , separadas por uma distância
, separadas por uma distância ![]() , sentem uma força dada por
, sentem uma força dada por
(2) 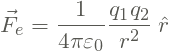
onde ![]() é uma constante também universal, ou seja, não depende da Natureza das cargas elétricas.
é uma constante também universal, ou seja, não depende da Natureza das cargas elétricas.
É interessante observar que a equação acima é muito parecida com a equação (1). Só precisamos fazer as correspondências
(3) 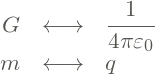
Mas há uma diferença fundamental entre as duas forças. Enquanto que na Natureza há somente um “tipo” de massa, cargas elétricas vêm em dois tipos: convencionamos chamá-las de carga positiva e carga negativa. Com isto, a força coulombiana pode ser atrativa (cargas opostas) ou repulsiva (cargas de mesmo tipo).
Se separarmos dois prótons a uma certa distância ![]() , qual deve ser a razão entre a força eletrostática e a força gravitacional?
, qual deve ser a razão entre a força eletrostática e a força gravitacional?
Como ambas as forças dependem do inverso do quadrado da distância [veja equações (1) e (2)], a razão dá
![Rendered by QuickLaTeX.com \[ \frac{F_e}{F_g} = \frac{1}{4\pi\varepsilon_0}\frac{1}{G}\frac{e^2}{m_p^2} \]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-80b204c6f798ac59daedf50b4556deca_l3.png)
Sabendo-se que a massa do próton é ![]() e a sua carga é
e a sua carga é ![]() e que
e que
![Rendered by QuickLaTeX.com \[ G = 6,\!67 \times 10^{-11} \textrm{m}^3 \textrm{kg}^{-1}\textrm{s}^{-2} \quad \textrm{ e } \quad \displaystyle \frac{1}{4\pi\varepsilon_0} = 8,\!99 \times 10^9 \textrm{m}^2 \textrm{C}^{-2} \]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-9539444ad4917f15f6be3acca994a267_l3.png)
no sistema internacional de unidades, temos que
![Rendered by QuickLaTeX.com \[ \frac{F_e}{F_g} \approx 1 \times 10^{36} \]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-5b1c5211891513d47f10f9c117aeeec3_l3.png)
Ou seja, a força eletrostática é muitíssimo maior do que a gravitacional.
Mas ainda bem que o Universo é um lugar mais ou menos neutro eletricamente, ou seja, a carga resultante é zero. Caso contrário, se tivéssemos só um tipo de carga, jamais seria possível formar planetas, estrelas, galáxias e todos os aglomerados de matéria, pois a força gravitacional seria insignificante dianta da força eletrostática repulsiva.
No entanto, como a matéria é praticamente neutra, a atração gravitacional dá origem às grandes estruturas do Universo.
Por outro lado, forças eletrostáticas são fundamentais na escala microscópica. Embora o modelo atômico vigente, descrito pela Mecânica Quântica, é incompatível em muitos aspectos ao modelo semiclássico como o átomo de Bohr, é bastante instrutivo pensar num modelo “planetário” para o átomo, onde elétrons em determinados orbitais giram em torno do núcleo formado por nêutrons e prótons.
Aqui abrimos um parêntesis para fazer um brainstorm: o que mantém os prótons coesos no núcleo, pois deveria haver repulsão entre eles? O que mantêm os nêutrons no núcleo, se eles são eletricamente neutros?
Prosseguindo, dá para se estabelecer um paralelo do modelo planetário com o modelo semiclássico do átomo. Enquanto no primeiro caso, a força gravitacional é a responsável pelas órbitas dos planetas, no segundo, é a força eletrostática (cargas estão sendo aceleradas, mas os postulados de Niels Bohr “cuidam” desses detalhes).


Para ambas as forças, surge uma questão curiosa: de que forma uma massa “sente” a presença de uma outra massa? Similarmente, como uma carga “sente” a presença da outra?
Na figura dos planetas orbitando o Sol, que “coisa” comunica a um planeta que o Sol está lá e vice-versa? Afinal, se o Sol desaparecer de repente, os planetas sairiam das suas órbitas!
Chamamos essa “coisa” de campo. Temos assim o campo gravitacional e o campo elétrico, onde discutiremos em maiores detalhes a seguir.
O Campo Elétrico
Assim como ocorre com as massas e a força gravitacional, como exatamente corpos e cargas elétricas interagem?
Não vemos nenhum tipo de contato entre, por exemplo, a Terra e uma maça que cai em sua direção. Também não ocorre o contato físico entre as cargas para existir a força elétrica, dada pela lei de Coulomb.
Num curso de Mecânica, introduzimos o conceito de aceleração da gravidade ![]() para descrever o movimento de queda de um corpo próximo à superfície de um planeta (especificamente a Terra). O objeto cai porque existe a força de atração objeto-Terra. Por aceleração da gravidade, entendemos que se trata da aceleração adquirida pelo corpo se desprezada a resistência do ar. Vejamos como ela surge.
para descrever o movimento de queda de um corpo próximo à superfície de um planeta (especificamente a Terra). O objeto cai porque existe a força de atração objeto-Terra. Por aceleração da gravidade, entendemos que se trata da aceleração adquirida pelo corpo se desprezada a resistência do ar. Vejamos como ela surge.
A força entre a Terra e o corpo é dada pela lei da gravitação universal de Newton [equação (1)]. É importante observar que a equação (1) pode ser facilmente adaptada para objetos extensos, em particular para uma esfera cuja densidade de massa só dependa da distância até o seu centro. Se essa é a força resultante sobre o corpo, a segunda lei de Newton afirma que
![Rendered by QuickLaTeX.com \[ F_g = -G \frac{M_T m}{(R_T+h)^2} = m a \quad \Rightarrow \quad a = -G \frac{M_T}{(R_T+h)^2} \]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-3483b3f0371f89c50274db6be8d67473_l3.png)
onde ![]() e
e ![]() são, respectivamente, a massa e o raio da Terra e
são, respectivamente, a massa e o raio da Terra e ![]() a altura em relação à superfície da Terra. Próximo à superfície da Terra,
a altura em relação à superfície da Terra. Próximo à superfície da Terra, ![]() (altura é muito menor do que o raio da Terra) e portanto
(altura é muito menor do que o raio da Terra) e portanto
![Rendered by QuickLaTeX.com \[ a \approx -G\frac{M_T}{R_T^2} \equiv -g \]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-0a8834bb452d5e4e8b18ca0f27b8cffc_l3.png)
Logo, a aceleração é ![]() . Por outro lado, temos que próximo à superfície da Terra, a força sobre um objeto de massa
. Por outro lado, temos que próximo à superfície da Terra, a força sobre um objeto de massa ![]() , dada pela equação (1) se torna
, dada pela equação (1) se torna
![]()
Usando a notação vetorial, temos que
![Rendered by QuickLaTeX.com \[ \vec{g} = \frac{\vec{F}_g}{m} \]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-1b0ff8d1b20c45d75c31929e69cd38c7_l3.png)
Encontramos a “coisa” que estávamos procurando: é ![]() , que se chama campo gravitacional da Terra (neste caso, próximo à sua superfície). Em qualquer região
, que se chama campo gravitacional da Terra (neste caso, próximo à sua superfície). Em qualquer região ![]() ,
,
![]()
onde ![]() denota que o campo gravitacional é radial e aponta para o centro da Terra. É claro, a massa
denota que o campo gravitacional é radial e aponta para o centro da Terra. É claro, a massa ![]() também produzirá um campo gravitacional, que a Terra e todos os objetos massivos, irão sentir.
também produzirá um campo gravitacional, que a Terra e todos os objetos massivos, irão sentir.
Mas afinal, o que é campo gravitacional? Está presente no espaço, mas não a vemos. Nós sentimos o seu efeito da seguinte forma: determine a força (gravitacional) que age num objeto de massa ![]() (módulo, direção e sentido). Divida essa força por
(módulo, direção e sentido). Divida essa força por ![]() e assim terá o campo. Dizemos que o campo gravitacional é o mediador da interação gravitacional. Qualquer coisa além disto, caimos numa discussão metafísica de campo.
e assim terá o campo. Dizemos que o campo gravitacional é o mediador da interação gravitacional. Qualquer coisa além disto, caimos numa discussão metafísica de campo.
Se fizermos a substituição da massa pela carga elétrica, nós obtemos algo que chamamos de campo elétrico. Para um sistema formado pelas cargas ![]() e
e ![]() , separadas por uma distância
, separadas por uma distância ![]() , temos pela lei de Coulomb que a força sobre a carga
, temos pela lei de Coulomb que a força sobre a carga ![]() é
é
![Rendered by QuickLaTeX.com \[ \vec{F}_{e} = \frac{1}{4\pi\varepsilon_0} \frac{q q_0}{r^2}\:\hat{r} = \left( \frac{1}{4\pi\varepsilon_0} \frac{q}{r^2} \: \hat{r} \right) q_0 \]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-ac0d28cf93ea7fbe3cb045e4b70d30f3_l3.png)
Analogamente à definição de ![]() , se dividirmos a força sobre
, se dividirmos a força sobre ![]() pela própria carga
pela própria carga ![]() , obtemos o termo entre parêntesis acima, que é precisamente o campo elétrico gerado pela carga
, obtemos o termo entre parêntesis acima, que é precisamente o campo elétrico gerado pela carga ![]() na posição onde se encontra
na posição onde se encontra ![]() :
:
(4) 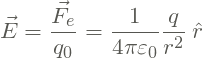
O campo elétrico, assim como o campo gravitacional, possui intensidade, direção e sentido, o que faz dele uma grandeza vetorial.
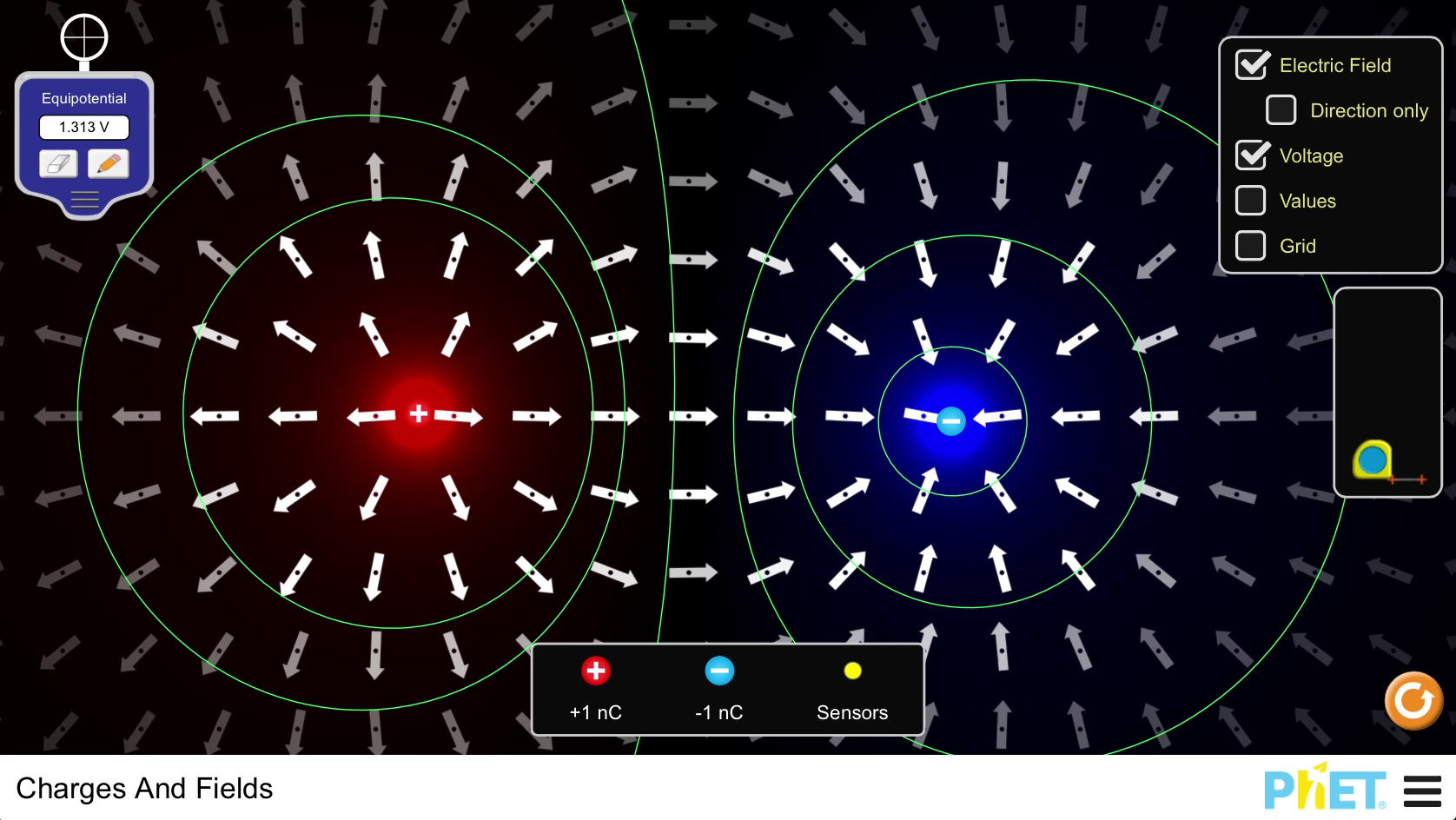
Representaremos o campo elétrico usando o que chamamos de linhas de campo. Elas são um pequeno número das possíveis infinitamente numerosas linhas que indicam o sentido e a direção do campo elétrico. O campo elétrico num determinado ponto é tangente à linha de campo.
Abaixo temos as linhas de campo representando o campo elétrico de uma carga positiva. As linhas são radiais apontando para fora. O campo elétrico também será radial, apontando para fora.

No caso da carga negativa, as linhas de campo são igualmente radiais, mas apontam para dentro. Logo, o campo elétrico também será radial e apontará para a carga.

Quando duas cargas elétricas de sinais opostos são colocadas próximas, seus campos elétricos passam a interagir, criando em suas proximidades uma configuração diferente da que observamos quando tais cargas encontra-se isoladas. O campo resultante é a soma (vetorial) dos campos de carga positiva e negativa.

No simulador disponível abaixo, você pode testar diferentes configurações de cargas elétricas, e observar as mudanças sofridas no espaço em torno das cargas elétricas.
Campo elétrico de uma distribuição de cargas
No Ensino Médio, só se calculam campos elétricos devido a uma distribuição discreta de cargas (cargas puntiformes). O campo elétrico resultante é a soma (vetorial) de todos os campos gerados pelas cargas puntiformes num determinado ponto do espaço. Achar o campo resultante torna-se assim, um problema de soma de vetores, cujo conhecimento de geometria ajuda bastante. Um exemplo comum é colocar uma determinada carga em cada um dos vértices de um retângulo e pedir o campo elétrico resultante em algum ponto do espaço (num vértice, no centro do retângulo, etc.)
Para essas distribuições, a determinação do campo elétrico resultante num ponto não é um problema desafiador. O que pode ser desafiador, mas que não está no escopo do Ensino Médio, é a obtenção do campo elétrico de uma distribuição contínua de carga. Por exemplo, qual seria o campo elétrico de uma barra delgada uniformemente carregada? E o campo de uma esfera metálica, cuja carga total se concentra inteiramente na sua superfície?
Esse questionamento também surge para o cálculo do campo gravitacional de objetos extensos. Por exemplo, se ao invés da Terra ser uma esfera, se fosse chata, como deveria ser o seu campo gravitacional? Como é o campo gravitacional dentro da superfície da Terra?
Na Física, há uma receita muito simples para esse tipo de configuração de carga. Vamos ilustrá-la com um exemplo; o cálculo do campo elétrico de um fio carregado e muito longo. Vamos denotar por ![]() a densidade linear de carga (quantidade de carga elétrica por comprimento do fio) .
a densidade linear de carga (quantidade de carga elétrica por comprimento do fio) .
Até aqui, vimos que o campo elétrico devido a uma carga puntiforme é dado pela equação (4). Por comodidade, vamos repeti-lo aqui:
![Rendered by QuickLaTeX.com \[ \vec{E} = \frac{1}{4\pi\varepsilon_0} \frac{q}{r^2} \: \hat{r} \]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-147ec95babe8f8d719de1d1129e2b59d_l3.png)
Localizado a uma distância que chamaremos de ![]() acima desse fio, existe um ponto P. Nosso objetivo é calcular o campo elétrico no ponto P gerado por essa distribuição de carga no fio.
acima desse fio, existe um ponto P. Nosso objetivo é calcular o campo elétrico no ponto P gerado por essa distribuição de carga no fio.

Vamos supor que o fio se encontra sobre o eixo ![]() . Tomamos um pedaço pequeno no fio, que na figura acima está pintado de vermelho. Chamemos esse tamanho de
. Tomamos um pedaço pequeno no fio, que na figura acima está pintado de vermelho. Chamemos esse tamanho de ![]() . Nesse pedaço, a quantidade de carga presente é
. Nesse pedaço, a quantidade de carga presente é
![]()
Aqui ![]() não tem conotação usual de “diferença”, ou seja, final menos inicial de uma certa grandeza. Se
não tem conotação usual de “diferença”, ou seja, final menos inicial de uma certa grandeza. Se ![]() , o pedaço se colapsa num ponto e portanto a equação (4) é válida:
, o pedaço se colapsa num ponto e portanto a equação (4) é válida:
(5) 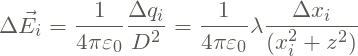
O campo acima só vale para um pedaço pequeno do fio, naquela posição específica. Como o fio é formado praticamente por uma quantidade muito grande desses pedaços pequenos e que para cada pedaço pequeno a equação (5) é válido, o campo resultante em P é a soma (vetorial) de cada um dos campos ![]() :
:
![Rendered by QuickLaTeX.com \[ \vec{E} = \sum \Delta \vec{E}_i = \sum_i^N \frac{1}{4\pi \varepsilon_0}\lambda \frac{\Delta x_i}{(x_i^2 + z^2)} \]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-d13ddd2c912e4504916ecafd6213caa7_l3.png)
Na linguagem do cálculo, no limite ![]() , faremos
, faremos ![]() , e o campo passa a ter um valor infinitesimal (muito pequeno) e o denotaremos por d\vec{E} (veja direção e sentido desse campo). Quando isso ocorre, a soma é substituída pela integral e os pontos discretos passam a ser contínuos:
, e o campo passa a ter um valor infinitesimal (muito pequeno) e o denotaremos por d\vec{E} (veja direção e sentido desse campo). Quando isso ocorre, a soma é substituída pela integral e os pontos discretos passam a ser contínuos:
![Rendered by QuickLaTeX.com \[ \vec{E} = \int d\vec{E} = \frac{1}{4\pi\varepsilon_0} \int \frac{dx \: \hat{r}}{x^2 + z^2} \]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-63bf15344fa6f2eb6623887275bec988_l3.png)
Um detalhe muito importante de integral é que ela é uma soma. E como estamos somando vetores ![]() , cuja direção muda conforme o
, cuja direção muda conforme o ![]() muda (o pedaço pequeno em vermelho no fio), é preciso tomar cuidado na hora de realizar a integral.
muda (o pedaço pequeno em vermelho no fio), é preciso tomar cuidado na hora de realizar a integral.
Para ver os detalhes técnicos e como resolver a integral, clique em “Abrir Dedução Matemática”.
O campo elétrico gerado por um fio de comprimento infinito num ponto P distante ![]() , será dado por
, será dado por
![Rendered by QuickLaTeX.com \[ E = \frac{1}{4\pi\varepsilon_)}\frac{\lambda}{z} \]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-84f36f775cd6fcc6350611d0274dcb24_l3.png)
Esse resultado obtido para o valor do campo elétrico gerado no espaço para um fio infinito, mostra um campo elétrico que cai com o inverso da distância. No caso de um campo gerado por uma carga pontual, como sabemos, o campo diminui com o quadrado do valor da distância.
É interessante notar que os campos estão intimamente relacionados com o espaço, e são invariáveis. Perceba que essa campo é calculado a partir de um referencial que está em repouso com relação ao fio. Iremos estudar a o caso do campo elétrico calculado a partir de um referencial que se movimenta com relação ao fio. Estudaremos assim sua invariabilidade com relação às transformações de Lorentz.