A Velocidade da Luz

Ao estudarmos as equações de Galileu e sua transformações, vimos que seus resultados se aplicam bastante bem aos problemas que envolvem o movimento de corpos. Esses resultados são bastante intuitivos para nós, por estarem de acordo com nossas experiências diárias. Como vimos que para o caso de um objeto em repouso inserido num referencial S’ que se move em relação a um observador num referencial S, as transformações que escrevemos são válidas se convenientemente aplicáveis.

Por outro lado precisamos saber se essas equações são coerentes com experimentos que envolvem a eletricidade, magnetismo e óptica.

James C. Maxwell já havia calculado ao final do século XIX, que qualquer radiação eletromagnética viaja no vácuo com uma velocidade de aproximadamente 300.000 Km/s.

Essa velocidade predita teoricamente para a velocidade da luz, era em relação a que? Em qual referencial deveria ser medida essa velocidade para que obtivéssemos esse valor como resultado?

Essa resposta não estava nas equações de Maxwell. 

Cientistas da época acreditavam que a luz e todas as radiações eletromagnéticas, assim como faziam as ondas mecânicas, necessitavam de um meio para se propagar. Em outras palavras, a luz viajava por um espaço preenchido por uma substância. Essa substância que preencheria todo o espaço, cuja existência foi teorizada, recebeu o nome de Éter.  

Se assim fosse, esperava-se obter diferentes valores para essa velocidade, dependendo do movimento do observador relativo ao meio no qual a luz se propaga. De outra forma, se um observador move-se com velocidade v em relação a esse meio, a medida da velocidade da luz poderia estar dentro de um intervalo que contemplasse um valor máximo (c+v) ou mínimo (c-v).

Se as transformações de Galileu pudessem ser aplicadas para a Luz, teríamos que para um observador que se move num referencial com velocidade v em relação ao éter, medidas para a velocidade da luz, valores que estariam compreendidos entre (c-v) e (c+v).

Suponha que estejamos viajando num supercarro que se desloca com velocidade de 150.000 km/s em relação a um observador em Terra. Esse carro seria ultrapassado por um feixe de luz com velocidade de 300.000 km/s medida pelo observador em Terra. A velocidade da luz medida pelo piloto do supercarro não seria de 300.000 km/s, mas sim de 150.000 km/s (300.000 km/s – 150.000 km/s).

Se isso fosse possível, teríamos um fenômeno acontecendo com ondas luminosas, análogo ao que ocorre com ondas sonoras. O estrondo sônico.

Pense no exemplo do avião supersônico que quando voa acima da velocidade de propagação do som para aquele meio. Este experimenta o estrondo sônico, um fenômeno que colapsa as frentes de onda umas sobre as outras e produz uma explosão sonora para observadores em Terra. Nesse caso do piloto do avião, a velocidade do som produzido pelo avião é medida pelo piloto como sendo zero, já que os piloto e onda sonora naquele meio deslocam-se com a mesma velocidade.

No vídeo abaixo você pode entender um pouco mais desse efeito chamado de estrondo sônico.

Pensando no caso da luz, seria possível que algum observador deslocando-se muito próximo da velocidade da luz, mediria uma velocidade diferente para ela? Seria possível ainda pensarmos em fenômeno similar ao estrondo sônico acontecendo com a luz?

Foi na tentativa de responder essas perguntas que inúmeros cientistas tentaram medir uma velocidade de propagação diferente para a luz do que aquelas previstas pelas equações de Maxwell.

Muitos experimentos foram realizados ao longo dos anos do século XVIII, e por conta da altíssima velocidade da luz, esses experimentos não eram precisos o suficiente para diferenciar uma velocidade medida como c ou c+v. Até que em 1880, os cientistas decidiram usar o movimento do planeta Terra na tentativa de obter melhores resultados.

Assumindo que o Sol estivesse em repouso com relação ao Éter, e que a velocidade da Terra ao orbitar o Sol é de 30 km/s, seria esperado que houvesse uma variação da velocidade medida para a luz de 1 parte em 10.000. Isso porque a velocidade da luz que seria de 300.000 km/s em relação ao éter, poderia variar entre 270.000 km/h e 330.000 km/h.

Após a segunda metade do Séc. XIX, dois experimentos destacaram-se na tentativa de caracterizar a natureza do Éter Luminífero. O primeiro deles realizado por Hippolyte Fizeau em 1851, e o experimento de Michelson – Morley. Ambos forma importantes na tentativa de detectar o Éter, contudo o experimento de Michelson – Morley foi o mais importante, e por essa razão ele será abordado a seguir.

O Experimento de Michelson-Morley

O mais notável e famoso experimento para detectar pequanas variações na velocidade de propagação da luz, foi realizado em 1881.

O experimento consistiu em medir a velocidade da luz aproveitando-se do movimento e da velocidade de translação da Terra utilizando-se um aparato que ficou conhecido como interferômetro de Michelson-Morley consistido de dois braços de mesmo comprimento, dispostos perpendicularmente entre si.

Na extremidade de um dos braços, uma fonte emissora de luz. Na intersecção dos braços um conjunto de espelho semi-transparentes posicionados de forma angulada em 45 º.

Nas extremidades dos dois braços espelhos refletores e um anteparo que permitia enxergar o feixe de luz refletido.

A idéia era separar em dois feixes de menor intensidade o feixe principal, fazendo com que refletissem separadamente e no seu percurso de volta, se unissem novamente exibindo no anteparo o feixe de luz re-combinado.

          Disponível na integra: https://youtu.be/UA1qG7Fjc2A

Para uma visualização completa da animação, o vídeo a seguir exibe além da trajetória da luz, uma representação do fenômeno da interferência típico de fenômenos ondulatórios.

Como os braços do interferômetro possuíam mesmo comprimento, a intensidade do feixe quando incidisse sobre o anteparo dependeria das interferências construtivas ou destrutivas apenas.

Vídeo sobre Interferência - Expandir

Se os feixes de luz tivessem diferentes velocidades em ambas as direções, padrões de interferência deveriam ser observados nos anteparos. Era isso que o experimento buscava comprovar.

De que forma? 

Pois bem vamos considerar que um dos feixes move-se numa direção paralela à de propagação do Éter. Como no exemplo do avião que voa contra o vento, a velocidade medida para a luz deveria ser portanto ao mover-se contra o Éter

Tomando como sendo o comprimento dos braços um valor de L, obteremos para o intervalo de tempo de ida do feixe de Luz

Tomando o tempo para o caminho de volta

O tempo total seria portanto

Calculando o tempo total para o feixe de luz que viaja perpendicularmente com relação ao Éter, teríamos

No caso do braço 2, aquele no qual a luz viaja perpendicularmente ao Éter, o valor para a velocidade resultante foi obtido utilizando-se o triângulo pitagórico.

A diferença de tempo para que os dois feixes percorram os seus respectivos caminhos, deverá ser dada pela diferença entre as expressões para cada braço.

Pelo fato de termos  v²/c² << 1, usaremos uma expansão binomial descartando os termos de grau maior do que 2

Por causa dessas substituição, temos

   

Como nosso valor para x = v²/c²

Que é a diferença de tempo entre a chegada ao anteparo dos dois feixes de luz.

Para se ter uma idéia de como seria esse efeito, a animação a seguir mostra utilizando pontos coloridos as diferenças de caminho para cada feixe de luz. Novamente, o feixe representado em azul precisa percorrer um caminho maior por viajar ao logo da direção do movimento orbital da Terra. Já o feixe vermelho, com velocidade perpendicular ao movimento orbital, sofre menor influência do movimento nessa direção, tendo seu tempo de chegada diminuído.

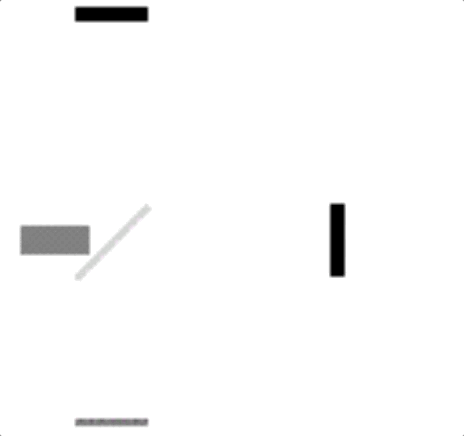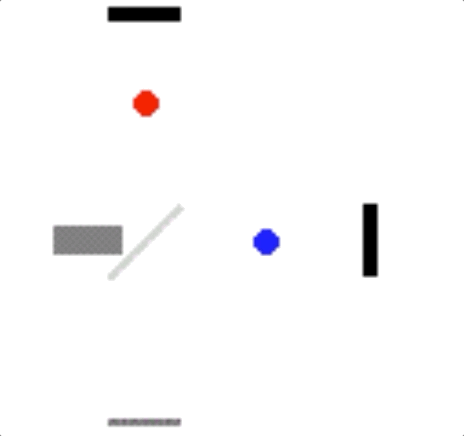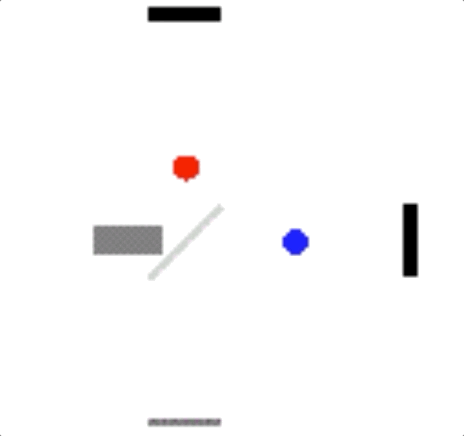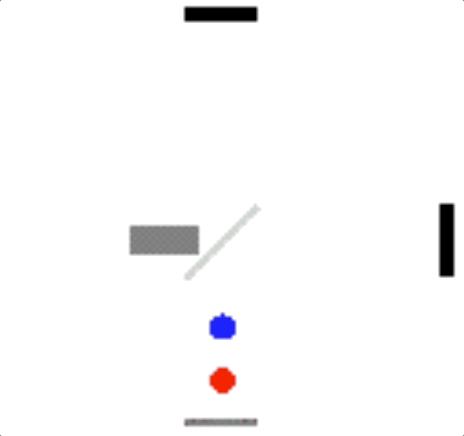
fonte: https://en.wikipedia.org/wiki/Michelson–Morley_experiment

Alguns questionamentos são importantes nesse ponto do experimento, como por exemplo a direção do movimento orbital da Terra, ou ainda imprecisões nos tamanhos dos braços utilizados no interferômetro.

Para que tais efeitos não produzissem resultados tendenciosos, o experimento foi girado de um ângulo de 90º e as medidas foram feitas nessa posição.

A diferença de tempo entre os dois instantes no qual os feixes refletidos chegam ao detector produzem uma diferença de fase entre esses feixes, ocasionando um padrão de interferência quando esses se recombinam no anteparo do detector.
Uma rotação de 90º sobre o interferômetro no plano horizontal, fará com que os dois feixes cheguem ao detector em posições alternadas. Essa rotação sobre o interferômetro resulta numa diferença de tempo que corresponde ao dobro do valor calculado acima. Por conta disso a diferença de caminho corresponde ao dobro da expressão obtida.

Essa diferença de caminho percorrida pelos dois feixes, poderia ser representada na forma de uma mudança na posição das franjas formadas no anteparo por conta da interferência devido à diferença de caminho.

Assim, poderíamos escrever a expressão na forma

Além disso o experimento foi repetido em diferentes estações do ano, pois é bem sabido que o sentido do movimento orbital da Terra se inverte a cada seis meses. Quando no verão a Terra viaja em uma direção e sentido, seis meses depois, no inverno, seu movimento e contrário. Assim se eventualmente o éter estivesse movimentando-se em relação à Terra em determinada época do ano, nos meses seguintes esse cenário seria diferente.

O valor estimado para esse desvio, utilizando-se um comprimento de onda de radiação bem conhecido e os tamanhos dos braços do interferômetro também conhecidos, seria de:

Com esse valor para o desvio, os cientistas A. Michelson e E. Morley esperavam encontrar um padrão de interferência destrutiva, já que trata-se de um número semi-inteiro. Em outras palavras, se houvesse uma velocidade relativa do aparato que viajava junto com a Terra, em relação à velocidade da luz, padrões de interferência destrutiva seriam observados.

A precisão do instrumento utilizado por Michelson e Morley podia detectar desvios da ordem de 0,01, muito menores portanto do que o desvio que se esperava obter.

O resultado obtido para o valor do desvio foi de zero.

O que foi observado pela falta de um padrão de interferência destrutiva entre as ondas.

Ainda assim a hipótese do Éter não foi descartada. Algumas explicações foram dadas na tentativa de justificar os resultados do experimento, nem todas elas satisfatórias.

Chegou-se a pensar que o Éter viajasse junto com a Terra, é por isso a detecção de uma interferência destrutiva causada pela mudança na velocidade de propagação da luz, não poderia ser percebida.

fonte: https://en.wikipedia.org/wiki/Michelson–Morley_experiment

A quantidade de “concessões” e explicações necessárias para salvar a idéia do Éter, era cada vez maior. Dizer que o éter movia-se junto com a Terra, ou ainda que a Terra carregava consigo o Éter, não parecia ser uma boa idéia. Novamente a situação assemelha-se pelo menos ideologicamente falando, às tentativas de salvar o modelo Geocêntrico proposto por Ptolomeu. A ideia de que a Terra estava no centro de alguma coisa, ou ainda de que a Terra constituía um referencial absoluto, soava cada vez mais estranha à medida que se sabia cada vez mais a respeito do universo.

Pouco tempo depois da realização do experimento, um físico irlandês pensou em uma possibilidade para dar conta de explicar o não aparecimento dos padrões de interferência destrutiva esperados. Seu nome era George Francis FitzGerald, e ele pensou em uma possível explicação para o ocorrido.

Segundo FitzGerald o padrão de interferência não pode ser observado por que as distâncias percorridas pelos dois feixes de Luz separados no interferômetro eram as mesmas. Como isso seria possível sem negar a existência do éter? Simples, FitzGerald pensou que por alguma razão desconhecida, o braço do interferômetro que apontava na direção do movimento da Terra, sofreria um encurtamento, ou seja uma diminuição no seu comprimento.

De outra forma, o que FitzGerald queria dizer é que se um corpo viaja com uma velocidade qualquer através do espaço, suas dimensões tendem a diminuir ao longo da direção para o qual o corpo se move. Pode parecer uma explicação estranha e até soar absurda, tanto é que poucos cientistas não aprovaram a explicação de FitzGerald.

A hipótese de FitzGerald necessitava de algo mais substancial. Isso aconteceu quando um notável matemático holandês de nome Hendrik Antoon Lorentz, propôs um conjunto de equações matemáticas que descreviam a tal contração pensada por FitzGerald.

As transformações de FitzGerald – Lorentz, como ficaram conhecidas, propunham uma justificativa para o fenômeno que causava a não detecção de interferência no equipamento. Com essa explicação a hipótese do éter poderia ser salva e a explicação para o fenômeno, por mais estranha que parecesse, passaria a ter um embasamento matemático.

Na página Relatividade Restrita – Equações da Transformação de Lorentz estão disponíveis as transformações propostas por FitzGerald – Lorentz. O fenômeno ficou conhecido pelo nome de Contração de Lorentz, e foi primeiramente previsto e descrito pelas equações e modelo matemático de FitzGerald – Lorentz.

Ainda como conseqüência das Transformações de Lorentz, surge a partir das equações a relatividade do tempo e o conceito de tempo local.

Embora os cientistas tivessem encontrado uma outra hipótese que justificasse a não detecção da interferência destrutiva entre as ondas, e conseguido um conjunto de transformações matemáticas que adequava-se ao fenômeno, a pergunta sobre a existência do éter permanecia não respondida. Se não fosse possível detectar o éter com qualquer experimento, como provar que ele de fato existia?

Por outro lado as Equações de Maxwell que não constituíam qualquer limitação àquilo que fora observado no experimento de Michelson-Morley.

Tampouco apresentavam quaisquer conflitos com as transformações de Lorentz, indicando a invariância de grandezas como por exemplo a própria velocidade da luz.

De modo bem direto, as equações concebidas por Maxwell, não necessitavam da existência de um meio para fazerem sentido. O Éter pensado primeiramente por Aristóteles e subsequentemente por vários outros cientistas no decorrer da história, era até então uma hipótese que não podia ser confirmada.

Em 1899 Henri Poincaré ao analisar os resultados obtidos pelo experimento de Michelson-Morley, propôs uma conjectura simples e geral para explicar o que ocorria ao se tentar medir a velocidade da luz. Ele dizia que o movimento absoluto não poderia ser detectado, ou seja, o movimento é algo relativo dependendo do referencial adotado.

O que Henri Poincaré havia percebido é que não seria possível existência de um experimento que fosse capaz de distinguir um estado de repouso absoluto de um estado de movimento uniforme, impossibilitando assim que qualquer experimento pudesse detectar algo como um movimento absoluto.

Esse princípio que já havia sido enunciado por Galileu, conhecido como princípio da relatividade.

A explicação plena levou alguns anos para aparecer, e embora tenha tido a contribuição de inúmeros cientistas, ela foi dada por Albert Einstein em 1905.

Albert Einstein, juntamente com as Transformações de FitzGerald-Lorentz, propôs a explicação que faltava.

A experiência de Michelson-Morley tem papel crucial na história da ciência e seu desfecho ajuda a sepultar a idéia de espaço e tempo como grandezas dissociáveis e absolutas. Abandonar essas concepções foi algo muito incômodo e difícil para a ciência da época, até porque de imediato não existia um modelo satisfatório que desse conta de explicar a aparente incoerência com a mecânica que se conhecia.

Na página disponível no link Postulados da Relatividade dá-se início à explicação proposta por Albert Einstein.

Acesso - Material Avançado - Abrir