Na dinâmica clássica ou não relativística, a força é definida matematicamente como sendo a variação do momento linear de um corpo, num dado intervalo de tempo.

A expressão abaixo é a forma matemática escrita em termos infinitesimais.

No site sobre Leis de Conservação, de autoria da Professora Ivânia de Oliveira, você encontrará uma dedução mais formal e desenvolvida dos conceitos de força e momento linear.

A discussão e análise que consta nessa página se concentrará em entender o que ocorre com um corpo ao receber a ação de uma força, quando sua velocidade é próxima da velocidade da luz.

As Leis de Newton para o movimento dos corpos apresenta uma bem sucedida expressão para o efeito de forças agindo sobre um corpo. A segunda Lei de Newton estabelece que a força aplicada sobre um corpo produz como resultado uma aceleração sobre esse corpo.

Para toda força aplicada sobre um corpo, lhe será imposta uma aceleração que dependerá do valor de sua massa.

Ocorre que essa lei não estabelece nenhum tipo de diferenciação sobre a velocidade com a qual um corpo se move, e menos ainda faz qualquer referência a um valor limite de velocidade, pois como sabemos essa lei foi estabelecida muito antes da concepção do trabalho de Albert Einstein.

Tal lei quando aplicada a corpos cujo atua uma força de intensidade constante, resulta num aumento linear da velocidade. Em outros termos, se uma força for permanecer aplicada sobre um corpo, aumentará sua velocidade indefinidamente enquanto essa força estiver presente. 

Existe um limite para a velocidade na natureza, e sabe-se que esse limite é a velocidade da luz. Corpos que possuem massa como uma grandeza intrínseca, podem andar bastante próximos da velocidade da luz, mas nunca viajar com tal valor.

A definição de força precisava ser reescrita propondo portanto, uma expressão mais genérica que englobasse todo o domínio de movimentos possíveis. 

Assim sendo, qual o efeito produzido sobre um corpo que viaja próximo da velocidade da luz, e sobre ele é aplicada uma força constante?

Para esclarecer esse questionamento, é retomada abaixo a definição de momento linear relativístico. O objetivo é encontrar uma expressão equivalente à força para o caso clássico.

A força é obtida calculando-se a função derivada do momento linear, com respeito ao tempo

Então

A expressão

tem a mesma direção do vetor velocidade.

O mesmo não ocorre com a expressão a seguir

que não necessariamente possuirá a mesma direção da velocidade.

Para abranger todos os casos possíveis, primeiramente será calculado o vetor força assumindo que ele seja paralelo à velocidade. 

Aplicando a regra do produto para a derivação, obtém-se

Utilizando a regra da cadeia para continuar a derivação

Observe o fator comum que pode ser extraído deixando a expressão mais sintética

Como

Então

Extraindo o denominador comum

A relação entre força e aceleração para o caso relativístico, o caso em que forças paralelas estejam atuando sobre o corpo está representado a seguir

Ficando estabelecido que essa é a expressão para a força no caso em que a velocidade e força tem mesma direção. Assim a seguinte notação se faz mais apropriada

A expressão guarda semelhanças com a segunda Lei de Newton, a diferença fica por conta do fator de Lorentz elevado ao cubo.

Em seguida será calculada a expressão para a força assumindo que a velocidade e a força não estão na mesma direção.

Novamente

A componente

terá valor nulo.

Restando apenas a componente sensível à direção perpendicular.

Assim, a expressão para a força em qualquer outra direção que não paralela, dependerá da direção de

O resultado para essa derivação é a expressão 

Como a expressão foi calculada para uma força perpendicular ao movimento, convém utilizar a notação para o módulo da força

Diferentemente da expressão para a aceleração obtida por Newton, as expressões derivadas das transformações de Lorentz apresentam diferenças sensíveis à direção da velocidade.

Enquanto que para a relatividade Newtoniana, a força aplicada sobre um copro possui as mesmas características qualquer que seja o referencial inercial de onde se observa a ação da força, para o caso das velocidades relativísticas, a força aplicada sobre um corpo tem valor diferente quando observada a partir de outros referenciais inerciais.

Ela continua obedecendo a segunda lei de Newton quando medida sobre a partícula em seu próprio referencial.

Continua também valendo para baixas velocidades, sendo esse efeito imperceptível.

Outra característica notável a ser observada é a de que forças que agem em direções perpendiculares à direção da velocidade de partículas relativísticas, também apresentam diferenças quando medidas a partir de dois diferentes referenciais.

Essas diferenças contudo, manifestam-se de forma diferente com relação à direção do movimento da partícula. Enquanto na direção do movimento as forças relacionam-se com um fator de , caso a força aplicada sobre a partícula venha a ter direção perpendicular ao seu movimento, quando medida de um referencial inercial no qual a partícula é relativística, o valor da força dependerá apenas de .

Com o objetivo de melhor clarificar esses conceitos, ao final da página, um exercício de aplicação é proposto com sua respectiva resolução.

Transformação da Aceleração

Do ponto de vista da dinâmica, foi possível obter expressões que relacionasse a força aplicada sobre um corpo medida em diferentes referenciais. As expressões obtidas, são mais genéricas e abrangem toda a gama de movimentos, tornando a já conhecida expressão para a 2ª Lei de Newton, um caso particular do estudo realizado.

Todavia, um questionamento bem relevante surge nesse ponto. Como ficariam as expressões para a aceleração de um corpo aplicando-se a definição às equações das transformações de Lorentz?

Assim, tomando as transformações de Velocidade de Lorentz como base, é possível estudar o comportamento da aceleração de um corpo à medida que esse corpo, aproxima-se da velocidade da luz.

Da mesma forma que para as transformações de velocidade de Lorentz, suponha uma partícula que viaja com velocidade , em um referencial que se move com velocidade , com relação a um referencial .

Novamente, tem-se para a direção

Aplicando a definição de aceleração, tem-se

Usando uma forma mais conveniente de notação

Definindo os elementos envolvidos na diferenciação

Seguem as diferenciais para as outras coordenadas

Como o que nos interessa é o valor da aceleração, podemos tomar como sendo zero o valor da velocidade do corpo no referencial S’.

As expressões para as diferenciais tornam-se mais simples

Aplicando a condição para as coordenadas restantes

Para encontrar a expressão para a aceleração, deve-se dividir a expressão diferencial para a velocidade, pela expressão diferencial do tempo. Utilizando-se a transformação de Lorentz para os instantes de tempo que relacionam os dois referenciais.

Tem-se para o tempo

E portanto, a diferencial

Evidenciando

De acordo com as condições iniciais descritas em (2.2), bem como para a definição, temos

Obtemos portanto

Aplicando a definição para aceleração fazendo uso das expressões diferenciais, tem-se

Calculando as componentes da aceleração nos outros dois eixos, obtém-se

As equações representadas, expressam os valores de aceleração medidos a partir de dois diferentes referenciais. Lembre-se que foi assumido o corpo estando inicialmente em repouso no referencial , sendo acelerado em seguida.

Nas transformações de Galileu, a aceleração é invariante quando se muda de um referencial para o outro, ou seja, ela é a mesma medida por qualquer outro observador contido em um referencial inercial.

Quando as velocidades dos corpos aproximam-se da velocidade da luz, a aceleração difere em magnitude medida em diferentes referenciais. Caso o corpo esteja acelerando em uma direção cujo sua velocidade inicial seja nula em ambos referenciais, a medida dessa aceleração também será diferente em ambos os casos.

Além disso, é possível notar que na direção do movimento inicial do corpo, a aceleração medida depende de um fator , enquanto que nas outras direções em que a velocidade inicial do corpo é zero em qualquer referencial, a aceleração depende de um fator .

Outra forma de representar as componentes da aceleração sem fazer uso das coordenadas, é substituí-las pela seguinte notação para a componente paralela à direção do movimento

E para as componentes perpendiculares

Em seguida será possível analisar que efeitos decorrem desses resultados, analisando a força aplicada sobre um corpo e a aceleração imprimida a ele.

Transformação de Força

O fato de a aceleração possuir diferentes coeficientes nas direções paralela e perpendicular ao movimento, traz conclusões importantíssimas para o estudo e compreensão de outros fenômenos.

Ainda de acordo com a transformação de Galileu a aceleração da partícula é a mesma quando medida a partir de quaisquer referenciais inerciais. Para um observador situado num referencial , a aceleração observada será a mesma observada por outro observador localizado num referencial .

Analisando o que foi concluído até agora, e estabelecendo um paralelo com a relatividade clássica, abaixo seguem as relações obtidas entre força e aceleração.

Para o caso clássico

Assim a força também poderá ser escrita nos dois referenciais de forma equivalente

Lançando mão da 2ª Lei de Newton, as forças nos dois referenciais estão relacionadas pela seguinte expressão

Para baixas velocidades, a força aplicada sobre um corpo será a mesma quando medida a partir de dois referenciais inerciais, portanto, valendo sobre elas as transformações de Galileu.

A situação se modifica quando o movimento dos corpos possui velocidades próximas às da luz, onde estão corretas as transformações de Lorentz. As equações de transformação para a aceleração para o caso em que uma partícula encontra-se em repouso junto ao seu referencial , foram apresentadas e novamente abaixo constam tais relações

Que é a expressão que relaciona as acelerações medidas em dois diferentes referenciais

Será tomado o movimento da partícula obedecendo algumas condições pré-estabelecidas. A partícula movimenta-se com velocidade na direção positiva de x () com respeito a um referencial inercial que a observa, estando ela em repouso no seu próprio referencial ().

Caso a partícula passe a acelerar, as expressões para tal já foram exibidas anteriormente. Abaixo, apenas estarão listadas as expressões decorrentes. Por exemplo, é possível obter a partir de:

Multiplicando pela massa , obtém-se

Lembrando da expressão já calculada que

No referencial em que a partícula encontra-se em repouso, de outra forma tem-se

Fazendo a substituição

Resulta na relação entre as forças em dois diferentes referenciais

Esse resultado mostra de que forma as forças medidas em dois referenciais diferentes relacionam-se, Observe que a componente da força que atua na direção do movimento é invariante nos dois referenciais, diferentemente da componente perpendicular ao movimento que sofre uma modificação proporcional à velocidade.

Mais uma vez, no caso em que a velocidade do corpo tende para o infinito, ou seja

Esse resultado mostra mais uma vez que quanto maior a velocidade de um objeto, mais a força medida difere com relação aos diferentes referenciais que observam esse movimento. 

As consequências das transformações de Lorentz sobre a aceleração e a força aplicada sobre um objeto podem ser relacionadas da seguinte forma:

• Para corpos viajando em altas velocidades, fica mais difícil de aumentar sua velocidade. Isso porque cada novo incremento de força aplicada sobre o corpo, surte apenas um pequeno efeito sobre sua aceleração.

     

• Quanto maior a velocidade com a qual um corpo viaja, medida a partir de um referencial inercial e para uma força finita aplicada, sua velocidade apenas se aproxima do valor limite que é de .
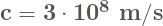• Quando um corpo viaja com velocidade próxima à velocidade da luz e sofre a ação de uma força, essa assume diferente valor quando observada de um outro referencial inercial. Essa diferença somente ocorre sobre a componente perpendicular ao movimento.
  

A conclusão obtida até aqui, tem profundas consequências sobre inúmeros fenômenos da natureza. O eletromagnetismo teorizado por Maxwell provê equações capazes de explicar o comportamento de cargas elétricas em repouso e movimento com base em quatro equações fundamentais. A interpretação dessas equações e sua relação com as transformações de Lorentz, leva ao que se chama de invariância. De outra forma, as equações de Maxwell são consonantes com as transformações de Lorentz, diferentemente das equações de Galileu.

Na página A Invariância das Equações de Maxwell nas Transformações de Lorentz é abordado um problema do eletromagnetismo, que ilustra o fato de a força elétrica e a força magnética descritas por Maxwell, possuírem uma relação com a relatividade de Einstein.

No problema proposto a seguir, uma discussão mais quantitativa é feita a respeito do comportamento da aceleração e força medidas a partir de dois diferentes referenciais. Um que viaja com velocidade igual a da partícula, e outro referencial que encontra-se em repouso no referencial do laboratório.

Problema

A massa de um elétron é de . Qual o valor da aceleração imprimida a esse elétron, se sobre ele estiver agindo uma força de  que atua na direção ? Considere o elétron observado a partir de um referencial no qual esse encontra-se em repouso.

Resolução

Utilizando a segunda lei de Newton

Que é o valor calculado para um corpo em repouso.

Considere agora o caso do mesmo elétron observado a partir de um referencial no qual ele possua a velocidade de  na direção . Qual a força que age sobre esse elétron quando medida a partir desse referencial?

Lembrando da relação

Na direção paralela ao movimento, a partícula não apresenta diferença no comportamento da força em ambos os referenciais, assim, a relação de interesse é aquela que diz respeito à componente perpendicular ao movimento.

Observe que a força medida no referencial em que a partícula encontra-se em movimento, é vezes menor do que aquela aplicada no referencial do corpo. Além disso ela tem direção perpendicular ao movimento.

Qual seria a aceleração desse corpo medida por um observador no referencial do laboratório, de acordo com as relações relativísticas entre massa e aceleração?

Comparando os resultados para a aceleração calculados nos dois referenciais, é possível notar ao relacionar os dois valores, que a aceleração medida a partir de um referencial no laboratório é cerca de 2500 vezes menor do que a aceleração medida no referencial cujo elétron encontra-se em repouso.