Como vimos, as equações de Galileu levam a resultados muito próximos dos resultados experimentais quando a velocidade dos corpos envolvidos é muito menor do que a velocidade da luz, ou seja quando temos ![]() .
.
Para velocidades maiores do que digamos ![]() , os efeitos relativísticos tornam-se suficientemente significativos de maneira tal que não podemos mais desprezá-los, sob a pena de não sermos capazes de prever corretamente as características e os resultados dos movimentos.
, os efeitos relativísticos tornam-se suficientemente significativos de maneira tal que não podemos mais desprezá-los, sob a pena de não sermos capazes de prever corretamente as características e os resultados dos movimentos.
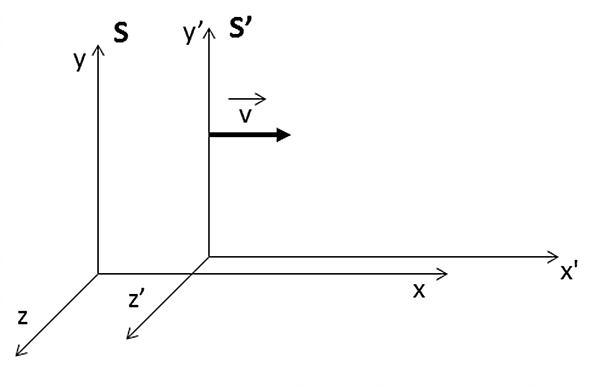
As equações que iremos estudar nessa página relacionam as coordenadas espaço-temporais de um evento em dois referenciais inerciais, que denotaremos por ![]() e
e ![]() . Tomaremos
. Tomaremos ![]() como sendo um referencial que se move com uma velocidade
como sendo um referencial que se move com uma velocidade ![]() constante em relação ao referencial
constante em relação ao referencial ![]() na direção do eixo
na direção do eixo ![]() positivo, e então escreveremos as equações do movimento para o caso das altas velocidades.
positivo, e então escreveremos as equações do movimento para o caso das altas velocidades.
Já fizemos isso uma vez para o caso clássico quando estudamos as equações do movimento de Galileu, e agora nessa página apresentaremos o que chamamos de Equações da Transformação de FitzGerald – Lorentz.
Para um objeto que está inserido num referencial ![]() na direção do eixo
na direção do eixo ![]() , as equações do movimento serão escritas na seguinte forma
, as equações do movimento serão escritas na seguinte forma
(1) 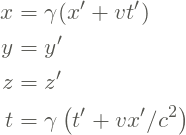
onde
![Rendered by QuickLaTeX.com \[ \gamma = \frac{1}{\sqrt{1-v^2/c^2}} \]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-f92fdcbdc05fcef01208258556ef2c39_l3.png)
Essas equações são muito parecidas com as equações de Transformações de Galileu, exceto por dois detalhes:
![Rendered by QuickLaTeX.com \[\begin{itemize} \item O fator $\gamma$, que depende essencialmente da raz\~ao $v/c$ \item O tempo \'e relativo, ou seja, depende do referencial e se mistura com as coordenadas de posi\c{c}\~ao e vice-versa. \end{itemize}\]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-64ed3aff7d8e2924668ffabdbac8f9e5_l3.png)
No entanto, observamos que se a velocidade ![]() de um referencial em relação a outro for muito menor do que
de um referencial em relação a outro for muito menor do que ![]() (
(![]() ),
),
![Rendered by QuickLaTeX.com \[ \gamma \to 1 \qquad \textrm{ e } \qquad \frac{v x' }{c^2} \to 0 \]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-82f768a829e262e4f497879c8d0c6444_l3.png)
de forma que as transformações de Lorentz levam às transformações de Galileu.
Se quisermos escrever as transformações inversas, isso é a partir do referencial ![]() , podemos obtê-las simplesmente intercambiando as variáveis espaço-temporais e alterando o sinal da velocidade, já que se trata-se de uma velocidade relativa.
, podemos obtê-las simplesmente intercambiando as variáveis espaço-temporais e alterando o sinal da velocidade, já que se trata-se de uma velocidade relativa.
Assim, obtemos as equações
(2) 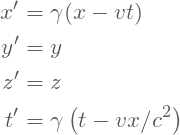
Consequência das Equações de Lorentz
A Não Simultaneidade dos eventos
Conforme já observamos, nas equações de Lorentz o espaço e o tempo aparecem entrelaçados. Isso traz consequências que desafiam o nosso senso comum
Consequentemente, um mesmo evento observado a partir de dois diferentes referenciais inerciais podem, e geralmente serão, não simultâneos.
Em nossas experiências diárias, tal afirmação ou ocorrência parece impossível e até ilógica. Imagine que você esteja jogando futebol num campo localizado próximo às margens de uma rodovia, e que em determinado momento você chuta a bola em direção ao gol e marca um tento a favor de seu time.
Não existem dúvidas de que você e seus amigos enxergaram o gol acontecendo ao mesmo tempo para todos, ou ainda simultaneamente.
E se ainda um carro estiver passando próximo do campo de futebol, na rodovia, e movendo-se com velocidade constante, e digamos ainda que o passageiro também observe o gol marcado por você, também não restará dúvidas de que no instante de tempo em que a bola entrou no gol, o passageiro do carro, você e os seus colegas de time concordam quanto à simultaneidade do ocorrido.
O que acontece é que em nossas experiências cotidianas, as velocidades envolvidas são extremamente pequenas se comparadas à velocidade da luz. Consequentemente, os efeitos de distorção do espaço-tempo não podem ser observados por nós.
Na relatividade restrita ou especial, chamamos de evento o fenômeno ocorrido no espaço-tempo e que pode ser percebido por um observador.
A definição do dicionário para a palavra evento tem alguns significados que podem ser empregados de acordo com sua utilidade.
No dicionário Michaelis On-line, os significados empregados para a palavras evento podem ser conferidos.
Michaelis On-line – Significado da palavra Evento
O significado que nos interessa é aquele que diz
ASTR Ponto no espaço-tempo de quatro dimensões.
Vimos que os intervalos de tempo medidos por dois observadores contidos em diferentes referenciais não serão necessariamente os mesmos, haja vista o fato de que o movimento relativo altera a dimensão espaço-tempo de maneira nem sempre igual para ambos. Dois eventos serão simultâneos para dois observadores se e somente se ambos estiverem contidos num mesmo referencial.
Isso pode ser constatado pela equação abaixo fazendo o intervalo de tempo medido no referencial S’ ser igual a zero, ou seja simultâneo nesse referencial
![Rendered by QuickLaTeX.com \[\Delta t = \gamma \left ( \Delta t'+\frac{v\Delta x'}{c^{2}} \right ) \rightarrow\ \Delta t'= 0 \]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-6ab6de96987e76a3d4cd0bb4479d85c7_l3.png)
Temos
![Rendered by QuickLaTeX.com \[\Delta t = \gamma \left ( \frac{v\Delta x'}{c^{2}} \right ) \left ( 2.1 \right )\]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-ebd6d3bc2ff1e1525515909a421f8c90_l3.png)
A equação (2.1) mostra que se num referencial S’ existe uma separação espacial entre dois eventos, eles não serão simultâneos em outro referencial. Perceba que a equação assume um valor para a diferença temporal diferente de zero no referencial S e independente da simultaneidade do referencial S’.
Imaginemos a seguinte situação:
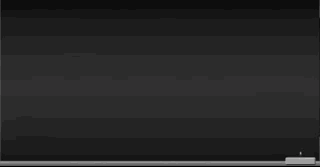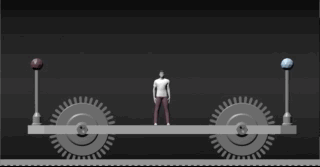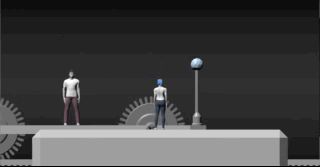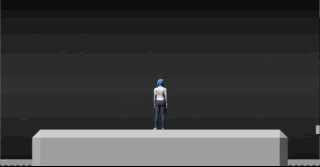
Uma mulher está parada em uma plataforma ferroviária. Em poucos instantes passará por ela, um homem a bordo de uma composição ferroviária, movendo-se com velocidade próxima à da luz.
Dentro desse vagão, existem duas lâmpadas, uma de cor azul e outra de cor vermelha, ambas podem ser acionadas para que pisquem sincronizadamente.
No exato momento em que o vagão do trem passa pela plataforma, as duas lâmpadas são acionadas de modo que os dois observadores recebem a informação luminosa.
Para a mulher que está na plataforma, no momento em que o trem passa por ela e emite os dois pulsos luminosos, ela os vê acendendo como representado na animação.
 Disponível na íntegra em https://youtu.be/KHFEFea70s4
Disponível na íntegra em https://youtu.be/KHFEFea70s4
No momento em que o trem passa pela mulher e as luzes acendem, ela está exatamente no meio do caminho entre as duas lâmpadas.
Por estar equidistante das duas fontes de luz, ela conclui que as lâmpadas acenderam simultaneamente, pois as luzes provenientes das lâmpadas, percorreram a mesma distância até ela viajando à mesma velocidade.
Chamaremos o acendimento das luzes de evento. Evento azul, e evento vermelho portanto.
A mulher observa então uma simultaneidade dos eventos. De seu ponto de vista, as duas lâmpadas piscaram ao mesmo tempo.
O que deverá ocorrer no referencial do homem então?
Perceba que em seu referencial, a luz também deve se deslocar com a mesma velocidade, vindo em sua direção pelos dois lados. O homem também está a meio caminho dos postes que emitem os pulsos luminosos.
Existe no entanto, uma diferença na condição dos dois observadores. O homem movimenta-se para a direita em relação à mulher e isso faz com que ele receba primeiro a informação do pulso luminoso de cor azul, isso porque esse pulso percorre uma distância menor até seus olhos, já que enquanto ele viaja para a direita junto com o trem, o pulso de luz azul viaja para a esquerda.
O pulso de cor vermelha no entanto, deve percorrer uma distância maior até seus olhos, pois o homem segue se afastando dele.
Embora as duas fontes de luz viajem juntas do trem, a velocidade de propagação da luz deve ser a mesma quando medida de qualquer referencial, não devendo ser somada ou subtraída. Teríamos a tendência de somar a velocidade do feixe vermelho à velocidade do trem por estarem viajando no mesmo sentido, e o contrário com o feixe azul por estarem em sentidos opostos. Isso está errado.
Os eventos azul e vermelho não são simultâneos no referencial do homem, o evento azul ocorre antes do evento vermelho.
Quem esta correto em sua observação?
A reposta é a de que os dois estão corretos. A única explicação plausível sugere que os eventos não são simultâneos para os dois referenciais. O piscar da luzes só pode ser simultâneo em um referencial.
 Disponível na íntegra em https://youtu.be/KHFEFea70s4
Disponível na íntegra em https://youtu.be/KHFEFea70s4
Essa é uma consequência da relatividade especial e dos postulados de Einstein. Qualquer informação leva um tempo finito para atingir um observador, e o movimento desse observador pode alterar a ordem na qual recebemos essa informação.
No link a seguir, a subpágina Mudança na Ordem dos Eventos dá acesso a um problema resolvido e comentado, extraído do Livro Fundamentos da Física, 10ª Edição, dos autores Halliday, Resnick e Walker. Nesse problema é discutido a não simultaneidade de dois eventos observados a partir de dois diferentes referenciais.
Clique aqui para seguir para a página As Transformações de Lorentz para a Velocidade.

![Rendered by QuickLaTeX.com \[\left\{\begin{matrix} A^{2}-c^{2}C^{2} = 1\\ \ \ \ A^{2}V+c^{2}BC = 0 \\ B^{2} - \frac{V^{2}}{c^{2}}A^{2} = 1 \end{matrix}\right.\]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-d198da6089498da1d7f325e3d5a28c7e_l3.png)
![Rendered by QuickLaTeX.com \[A^{2} = -\frac{c^{2}}{V}BC\]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-9d94f3f71981ba930643f972635a8849_l3.png)
![Rendered by QuickLaTeX.com \[\left.\begin{matrix} -c^{2}\frac{C}{V}\left ( B+VC \right ) =1\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ B^{2}+VBC = B\left ( B+VC \right ) = 1 \end{matrix}\right\}\]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-640c91a2c042951098efaa1f8da95f13_l3.png)
![Rendered by QuickLaTeX.com \[B = -\frac{c^{2}}{V}C\]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-6fc7b85197826584dfb65729e7559018_l3.png)
![Rendered by QuickLaTeX.com \[B^{2} - \frac{V^{2}}{c^{2}}A^{2} = 1\]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-3b830e7f8a157eb00e63fa5ec326bbfa_l3.png)
![Rendered by QuickLaTeX.com \[A^{2}\left ( 1-\frac{V^{2}}{c^{2}} \right )=1\]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-5823731168e7b90a7ca7b502f8e08a8c_l3.png)
![Rendered by QuickLaTeX.com \[\beta \equiv \frac{V}{c}\ \ \ \ \ \ ;\ \ \ \ \ \ \ \gamma \equiv \frac{1}{\sqrt{1-\beta ^{2}}}\]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-2b96887f4d8658a82733970dfe4d3efd_l3.png)