Momento Linear Relativístico

Na subpágina “Transformação de Coordenadas” dentro da página “Relatividade Galileana”, mostramos através de um exemplo simples que num processo de colisão entre dois corpos, o momento linear total do sistema se conserva, independentemente do referencial em que se observa a colisão.

O primeiro postulado de Einstein diz também que a Física deve permancer a mesma em todos os referenciais inerciais. Logo, no caso de uma colisão dita relativística, em que as velocidades dos corpos envolvidos na colisão são grandes, é esperado também que a conservação do momento linear seja verificada em todos os referenciais inerciais.

Classicamente, o momento linear de uma partícula de massa $m$ e velocidade $\vec{u}$ é definido como sendo

$\vec{p} = m \vec{u}$

No entanto, é possível mostrar que se adotarmos essa expressão e consideramos um processo de colisão, a conservação do momento linear verificada num referencial inercial não será verificada num outro, após a aplicação das transformações de Lorentz.

Por conta dessa aparente incoerência e pelo fato de termos assumido que as transformações de Lorentz para a velocidade estão corretas, devemos modificar, portanto, a expressão para o momento linear.

O momento linear relativístico é definido como sendo

$\vec{p} = \frac{m \vec{u}}{\sqrt{1-u^2/c^2}} = \gamma m \vec{u}$

Para corpos com velocidade baixa, $u \ll c$ , a expressão clássica reduz-se à forma clássica.

Força e a Segunda Lei de Newton na Relatividade

Conforme visto na subpágina “Mecânica Newtoniana” (clique aqui), a segunda lei de Newton pode ser expressa como sendo

(1) $\begin{equation*} \vec{F} = \frac{d\vec{p}}{dt} \end{equation*}$

Para um sistema de $N$ corpos, a força resultante é

$\vec{F}_\textrm{res} = \frac{d\vec{P}}{dt} = \frac{d}{dt}\left(\vec{p}_1 + \vec{p}_2 + \ldots \right) = \sum_{i=1}^N \frac{d\vec{p}_i}{dt}$

Num processo de colisão, a força resultante, que é a força externa, deve ser zero:

$\vec{F}_\textrm{res} = 0 \qquad \Rightarrow \qquad \vec{P} = \textrm{constante}$

ou seja, o momento linear total do sistema se conserva. Logo, a segunda lei de Newton dada pela Eq. (1) continua valendo para o caso relativístico. Por outro lado, é possível mostrar que as transformações de Lorentz deixa invariante a conservação do momento linear, sendo portanto consistente com o primeiro postulado de Einstein.

Apesar da Eq. (1) permanecer igual à expressão clássica, algo “estranho” deve ocorrer. Vejamos: o efeito de uma força sobre um corpo é produzir aceleração. Por exemplo, uma força constante produz uma aceleração constante (supondo aqui que a massa do objeto permaneça constante). Classicamente, podemos ter velocidade tendendo a infinito! Mas a relatividade diz que $u < c$ ! Como deve ser a expressão da força relativística?

Para responder a esta pergunta, “basta” derivarmos a Eq. 1 para $\vec{p} = \gamma m \vec{u}$ .

Temos que

$\vec{F} = \frac{d}{dt}( \gamma m \vec{u}) = \frac{d\gamma}{dt}m \vec{u} + \gamma m \frac{d\vec{u}}{dt}$

Mas,

$\frac{d\gamma}{dt} = \frac{d}{dt}\frac{1}{\sqrt{1-u^2/c^2}} = \frac{\vec{u}\cdot d\vec{u}/dt}{c^2\left(1-u^2/c^2\right)^{3/2}} = \gamma^3 \frac{\vec{u}\cdot d\vec{u}/dt}{c^2}$

Encontramos para a força relativística,

$\vec{F} = \gamma^3 \frac{m(\vec{u}\cdot \vec{a})}{c^2} \vec{u} + \gamma m \vec{a}$

onde a aceleração é simplesmente a derivada da velocidade em relação ao tempo:

$\vec{a} = \frac{d\vec{u}}{dt}$

Trata-se de uma expressão um tanto complicada. O primeiro termo da força é proporcional ao vetor velocidade $\vec{u}$ (o termo entre parêntesis é uma grandeza escalar). Observamos portanto que se $\vec{u}$ não estiver na direção de $\vec{F}$ , força e aceleração não estarão na mesma direção!

Vamos considerar uma situação bem mais simples, onde o corpo se movendo em uma direção, digamos sobe o eixo $x$ . Neste caso, a equação acima se reduz a

$F = \frac{m a}{\left(1-u^2/c^2 \right)^{3/2}} \quad \Rightarrow \quad a = \left(1-u^2/c^2 \right)^{3/2} \frac{F}{m}$

A fórmula acima mostra que se a força for constante, a medida que a velocidade vai tendendo à velocidade da luz, a aceleração vai a zero! Ou seja, a expressão é consistente com o segundo postulado de Einstein.

Energia Relativística

A Relatividade Restrita prevê, como vimos, por meio de seus postulados uma mudança completa na estrutura do espaço-tempo. O que antes era entendido como algo imutável, estático e fixo, ganha uma conotação diferente adquirindo o status de maleável, deformável.

Se foi preciso uma modificação nas definições de momento de uma partícula, então consequentemente será preciso uma modificação nas expressões que representam a energia do corpo, em particular, a energia cinética, isso porque essa energia está relacionada com o momento linear da partícula. Classicamente, a energia cinética é

$K = \frac{1}{2} m u^2 = \frac{p^2}{2m}$

Classificamente, essa fórmula vem do teorema do trabalho-energia cinética, que diz que o trabalho de uma força resultante sobre um corpo é igual à sua variação de energia cinética:

$W = \Delta K = \frac{1}{2} m u_2^2 - \frac{1}{2} m u_1^2$

Usaremos a letra $W$ para denotar o trabalho por causa da palavra work, do inglês.

É bom lembrar que “trabalho” em física significa transferência de energia para um corpo ou sistema (ou de um corpo ou sistema) que se desloca sob influência de uma força ou mais forças que agem sobre ele. Mais especificamente, somente a componente na direção do deslocamento realiza trabalho (lembre-se, por exemplo, que a força normal nunca realiza trabalho).

Como discutiremos a energia relativística, mostramos ao visitante interessado como se demonstra esse teorema.

Em uma dimensão, se uma força $F$ que atua na direção do deslocamento do corpo, de $x_1$ para $x_2$ , for constante, o trabalho é definido como sendo

$W = F (x_2 - x_1) = F \Delta x$

Caso a força não seja constante (caso da força elástica da mola),

$W = \int_{x_1}^{x_2} F \: dx$

Como

$F = \frac{dp}{dt} = m\frac{du}{dt},$

substituindo essa expressão na integral, obtemos

$W = m \int_{x_1}^{x_2} \frac{du}{dt} \: dx$

Usando uma propriedade de cálculo chamada “regra da cadeia”, observamos que os termos dentro da integral podem ser escritos como

$\frac{du}{dt} \: dx = \frac{du}{dx} \frac{dx}{dt} dx = u\left(\frac{du}{dx} dx\right) = u du$

onde evidentemente $u=dx/dt$ é a velocidade do corpo. Aí, a variável de integração será em $u$ , de $u_1$ até $u_2$ , onde $u_1 (u_2)$ é a velocidade quando o corpo está na posição $x_1$ ( $u_2$ ):

$W = m \int_{u_1}^{u_2} u du = \frac{1}{2} m u_2^2 - \frac{1}{2} m u_1^2$

ou seja,

$W = \Delta K = \frac{1}{2} m u_2^2 - \frac{1}{2} m u_1^2$

que é o teorema do trabalho-energia cinética.

Para obter o teorema trabalho-energia cinética, utilizamos a expressão clássica do momento linear. No entanto, se utilizarmos o momento linear relativístico, o que obteremos para $W$ ?

Deixamos a dedução matemática somente para os interessados.

Seguindo o mesmo caminho usado para demonstramos o teorema trabalho-energia cinética,

$W = \int_{x_1}^{x_2} F \: dx = \int_{x_1}^{x_2} \frac{dp}{dt}\: dx$

O momento relativístico é dado por

$p = \gamma m u = \frac{mu}{\sqrt{1-v^2/c^2}}$

Então, conforme já vimos acima, em uma dimensão temos que

$\frac{dp}{dt} = \frac{d}{dt}(\gamma m u) = \gamma^3 m \frac{du}{dt}$

Segue portanto que o trabalho fica

$W = \int_{x_1}^{x_2} \frac{m}{\left(1-u^2/c^2\right)^{3/2}} \frac{du}{dt} dx$

Mas similarmente à dedução clássica,

$\frac{du}{dt} dx = u du$

Logo,

$W = m \int_{u_1}^{u_2} \frac{u du}{\left(1-u^2/c^2 \right)^{3/2}} = \frac{mc^2}{\sqrt{1-u_2^2/c^2}} - \frac{mc^2}{\sqrt{1-u_1^2/c^2}}$

Temos que a versão relativística do teorema trabalho-energia cinética é dada por

$W = \Delta K = K_2 - K_1 = \frac{mc^2}{\sqrt{1-u_2^2/c^2}} - \frac{mc^2}{\sqrt{1-u_1^2/c^2}}$

Mas será que é correto atribuir

$K = \frac{mc^2}{\sqrt{1-u^2/c^2}} \qquad (???)$

Vamos supor que $u_1=0$ , ou seja, numa dada posição (ou tempo) inicial o corpo está em repouso, portanto ele não terá energia cinética ( $K_1=0$ ). Quando partícula atingir um ponto 2 com velocidade $u_2$ , de acordo com a equação obtida acima, a sua energia cinética será

$K_2 = \frac{mc^2}{\sqrt{1-u_2^2/c^2}} - mc^2$

Perceba que essa expressão possui um termo independente da velocidade do corpo. Chamaremos esse termo de energia de repouso do corpo, ou seja, encontramos a famosa equação de Einstein,

$E_0 = mc^2$

Se a energia cinética é $mc^2/\sqrt{1-u^2/c^2} - E_0$ , então é conveniente definir o primeiro termo como sendo a energia total do corpo:

$E_\textrm{total} = \frac{mc^2}{\sqrt{1-u^2/c^2}} = \gamma m c^2$

Em resumo, para um corpo de massa $m$ e velocidade $u$ ,

$E_\textrm{total} = \gamma m c^2$	energia total
$E_0 = m c^2$	energia de repouso
$K = E_\textrm{total} - E_0 = (\gamma -1) mc^2$	energia cinética

Massa relativística versus massa de repouso

Observe que a energia total do sistema é

$E_\textrm{total} = \gamma m c^2$

Em épocas passadas, era comum se referir ao termo $\gamma m$ como sendo a massa relativística do corpo. A medida que a velocidade do corpo aumenta, aumenta o valor de $\gamma$ e portanto dessa “massa relativística”.

É importante observar que na linguagem moderna, principalmente a comunidade de Física de Partículas, só atribui o conceito de massa quando essa quantidade é medida no seu referencial de repouso, pois se trata de uma quantidade instrínseca do objeto.

O que se interpreta é que a medida que a velocidade do objeto aumenta, aumenta o o fator $\gamma$ e portanto a energia do objeto aumenta e a massa permanece constante.

Equivalência massa-energia

Vamos voltar para a famosa equação de Einstein:

$E_0 = mc^2$

Trata-se de uma equação bastante simples, mas que carrega um aspecto conceitual bastante profundo. Como $c^2$ é meramente uma constante, ela diz essencialmente que massa nada mais é do que uma manifestação particular de energia. Trata-se da equivalência massa-energia.

Mas essa energia, a massa, pode se transformar em outras formas de energia?

Por volta de 1774, o químico Antoine Lavoisier conduziu experimentos cuidadosos e a partir dos resultados, concluiu que numa reação química ocorrendo num sistema fechado, a massa permanece constante, ou seja, a soma das massas dos reagentes é igual à soma das massas dos produtos:

massa dos reagentes = massa dos produtos

Trata-se da famosa Lei de Conservação de massa de Lavoisier.

Com instrumentos muito mais precisos e sobretudo analisando diferentes reações, por exemplo, uma reação nuclear, a massa não é uma grandeza que se conserva em processos atômicos e subatômicos.

Evidentemente, classicamente ou macrocospicamente, a massa é conservada. Se um carro se despedaçar numa violenta colisão, a soma das massa de todas as peças que se soltaram será igual a massa do carro intacto!

Essa constatação óbvia geralmente não ocorre em processos atômicos e subatômicos, como veremos no exemplo abaixo.

Exemplo 1: fissão do urânio

Em reatores de usinas nucleares utiliza-se um processo de produção de energia por meio de um fenômeno físico chamado fissão nuclear. Temos como exemplo o caso do $^{235}\textrm{U}$ que é usado como combustível nuclear em plantas nucleares. O átomo desse isótopo de urânio captura um nêutron livre, formando o $^{236}\textrm{U}$ , que sendo instável, sofre uma fissão nuclear (quebra do núcleo ou decaimento), através da seguinte reação:

$^{1}_0\textrm{n} +\, ^{235}_{92}\!\textrm{U} \to \,^{236}_{92}\!\textrm{U} \to \,^{141}_{56}\!\textrm{Ba} + \,^{92}_{36}\!\textrm{Kr} + \,3 ^{1}_0\!\textrm{n}$

Consultando o site http://periodictable.com/ encontramos as seguintes massas, em unidade de massa atômica, u:

$m(^{236}\textrm{U}) = 236,\!045568006\textrm{ u}; \quad m(^{141}\textrm{Ba}) =140,\!914411009\textrm{ u} ; \quad m(^{92}\textrm{Kr} ) = 91,\!92615621\textrm{ u} \quad \textrm{e}\quad m(\textrm{neutron}) = 1,\!00866491588\textrm{ u}$

A diferença entre as massas inicial e final é dada por

$\Delta m = m_\textrm{inicial} - m_\textrm{final} = m(^{236}\textrm{U}) - [m(^{141}\textrm{Ba})+ m(^{92}\textrm{Kr} ) + 3 m(\textrm{neutron})] \approx 0,\!1809 \textrm{u}$

Logo, a energia liberada é da ordem de

$E = \Delta m c^2 \approx (0,\!1809 \textrm{u}) c^2 \approx 170\textrm{ MeV}$

onde M $= 10^6$ e 1 eV $\approx 1,\!6 \times 10^{-19}$ J.

Pode parecer pequena, mas vale lembrar que essa é a energia liberada pela fissão de um único átomo de urânio. Para um mol, tem-se

$E_{mol} = N_A E = (6,\!022\times 10^{23}).(2,\!72 \times 10^{-11}\textrm{ J}) \approx 2 \times 10^{13} \textrm{ J}$

que é uma energia muito grande.

O que é e para onde vai essa energia liberada?

Essa energia está disponível em forma de energia cinética dos fragmentos gerados pela fissão. Ela é absorvida conforme os fragmentos se movem através da água, fazendo com que a energia interna da água aumente, elevando sua temperatura. O vapor d’água gerado no processo é usado para a geração de eletricidade.

Exemplo 2: fusão nuclear no interior do Sol

Outro fenômeno que envolve a conversão de uma certa quantidade de massa em energia é um processo chamado fusão nuclear, que ocorre comumente no interior de estrelas – o Sol, em particular.

O Sol é uma estrela considerada mediana, tanto em tamanho como brilho, sendo constituído 70% do elemento hidrogênio. O seu núcleo possui uma
densidade igual a 150 vezes a densidade da água líquida e uma temperatura de 15 milhões de
graus Celsius, com uma pressão de 26.5 Ppa (petapascal), de forma que o hidrogênio se encontra na forma de um gás de plasma, que corresponde a hidrogênio ionizado (ou seja, prótons e elétrons dissociados).

O principal mecanismo de produção de energia do Sol é a fusão nuclear conhecida como ciclo próton–próton (ciclo $pp$ ), ou cadeia $pp$ . O ciclo $pp$ é uma série de reações nucleares que transforma quatro núcleos de hidrogênio (próton) em um núcleo de $^4$ He, liberando fótons, partículas beta, neutrinos e energia, conforme a reação

$6\; ^1\textrm{H } \rightarrow \; 2 \textrm{ fotons} + 2 \textrm{ neutrinos} + 2\; ^1\textrm{H } + 2 \textrm{ positrons} + \; ^{4}\textrm{He}$

também ilustrada na figura abaixo:

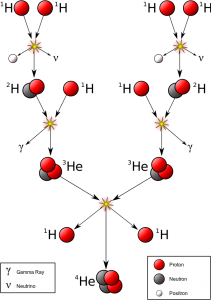
Fonte: https://en.wikipedia.org/wiki/Proton-proton_chain_reaction.

Para saber e entender um pouco mais sobre estrelas e seus processos, assista o vídeo abaixo:

Para se ter uma idéia da magnitude desse número, se tomarmos apenas 1 grama de matéria e fizermos esse cálculo novamente, obteremos um espantoso 10¹²J.

Tomando o equivalente em Joules de uma unidade de medida muito útil para nós, o KWh (quilowatt-hora), podemos comparar

$1 KWh = 3,6\cdot 10^{6}\ J$

Utilizando uma simples regra de três, obtemos

$3,6\cdot 10^{6}\ J - 1 KWh$

$1,0\cdot 10^{12} \ J- X$

$X = 2,8\cdot 10^{5} \ KWh$

São quase 300.000 KWh !

Para se ter uma idéia dessa quantidade de energia, numa residência onde reside uma família de 4 pessoas, o consumo médio por residência no ano de 2017 foi de 157 Kwh/mês,
(Fonte: https://istoe.com.br/consumo-de-energia-cresce-08-em-2017-primeira-alta-em-tres-anos/).

Utilizando como base esse valor de consumo e conhecendo a quantidade de energia liberada na fusão nuclear, podemos calcular quantas residências poderiam ser supridas.

Basta dividir a quantidade total de energia disponível, pelo consumo mensal por residência

$N\'umero\ de \ Resid\^encias =\frac{2,8\cdot 10^{5}}{157}\approx 1800 \ Resid\^encias$

Exemplo 3: decaimento radioativos

Um fenômeno natural no qual pode se observar as transformações envolvendo quantidades de massa em energia, são os decaimentos radioativos. Elementos químicos pesados, e temos como exemplos aqueles com os números atômicos mais altos presentes na tabela periódica, possuem um núcleo instável dando origem ao que chamamos de radioatividade. Como exemplo de elemento radioativo temos o Polônio (²¹⁶Po) que quando de seu decaimento dá origem a um núcleo de chumbo (²¹²Pb) . No processo também ocorre a emissão de uma partícula alfa (α), sendo essa um núcleo de Hélio (⁴He).

As massas dos elementos envolvidos, em unidade de massa atômica são:

(²¹⁶Po) = 216,001915 u
(²¹²Pb) = 211,991898 u
(⁴He) = 4,002603 u

a) Vamos calcular a mudança no valor da massa do sistema por conta do decaimento

$\Delta m = 216,001915\ u - (211,991898 \ u \ +\ 4,002603 \ u )$

Lembrando que u corresponde a uma grandeza chamada unidade de massa atômica, definida como sendo (1/12) da massa do átomo de Carbono.

Assim sendo

$u = 1,659023\cdot 10^{-27}\ Kg$

Então

$\Delta m = 0,007414\ u = 1,23\cdot 10^{-29}Kg$

b) Vamos calcular agora, qual será a energia associada à mudança de massa

$E= \Delta mc^{2} = (1,23\cdot 10^{-29}Kg)\cdot (3,00\cdot 10^{8}\ m/s)^{2}$

$E = 1,11\cdot 10^{-12}\ J = 6,92\ MeV$

Na applet abaixo, você pode simular o decaimento radioativo do Polônio e observar a emissão de partículas alfa.

A Física das partículas subatômicas estuda entre outras coisas, os fenômenos chamados radioativos.

A Radioatividade e seu estudo tem vital importância uma vez que muitos países no mundo utilizam como fonte de produção de energia elétrica, a energia nuclear. O Brasil possui uma planta nuclear localizada no litoral sul do Estado do Rio de Janeiro, mais precisamente na cidade de Angra dos Reis.

Plantas nucleares são uma opção ao abastecimento de energia num planeta com uma demanda energética cada vez maior, porém apresentam como forte contraponto a produção de resíduo nuclear tóxico.

Outro risco associado à sua implementação, é de que acidentes ocorridos nessas plantas quando estão em atividade, acabam liberando grandes quantidades de radiação no meio ambiente, devido ao vazamento do combustível nuclear utilizado.

No vídeo abaixo você pode aprender um pouco mais sobre como funcionam os reatores nucleares.