O campo elétrico como vimos é uma propriedade da carga elétrica podendo ser pensado como uma perturbação do espaço que contém a carga elétrica.
Porém existe outra manifestação da natureza que está relacionada ao sim à existência do Campo Elétrico, mas não pode ser explicado por ele. Estamos falando do Magnetismo.
O Magnetismo é uma propriedade que alguns materiais possuem de atrair objetos. Estamos falando dos populares ímãs. São basicamente minerais encontrados na natureza que possuem a capacidade de atrair objetos feitos de ferro, ou feito de partes de ferro.
Entre os ímãs que podem ser facilmente encontrados estão os feitos de Magnetita () e os ímãs de neodímio-ferro-bromo (
), popularmente chamados de ímãs de Terras Raras.
Além da capacidade de atrair outros materiais, é propriedade do ímã possuir duas regiões distintas que chamamos polos magnéticos. Essas regiões recebem o nome de polo norte e polo sul.
Tais regiões são identificadas através das interações que produzem. Polos de mesmo nome repelem-se enquanto que polos de nomes diferentes atraem-se.
Observe
Da mesma forma que identificamos nos campos elétricos as linhas de força relativas às cargas elétricas faremos também com ímãs. São atribuídas aos polos linhas de campo com um sentido de acordo com a polaridade. Dizemos que as linhas de campo de um ímã são fechadas num caminho que liga o Polo Norte do ímã até seu Polo Sul, exatamente nesse sentido. Usando uma linguagem mais corriqueira dizemos que as linhas de campo “deixam” o Polo Norte de um ímã e “chegam” no Polo Sul.
O polos de um ímã receberam esse nome por causa do que acontece quando o prendemos pela seu meio usando um barbante por exemplo, e fazendo-o suspenso no ar, ele girará alinhando-se imediatamente na direção dos polos magnéticos da Terra.
Abaixo uma figura representativa de um ímã em formato de barra e suas linhas de Campo Magnético.
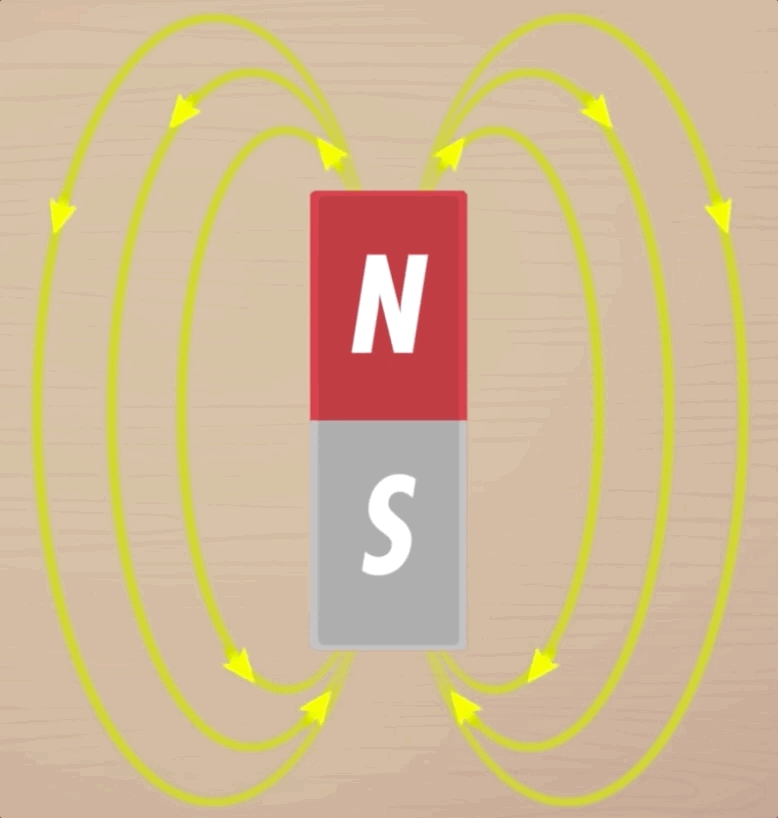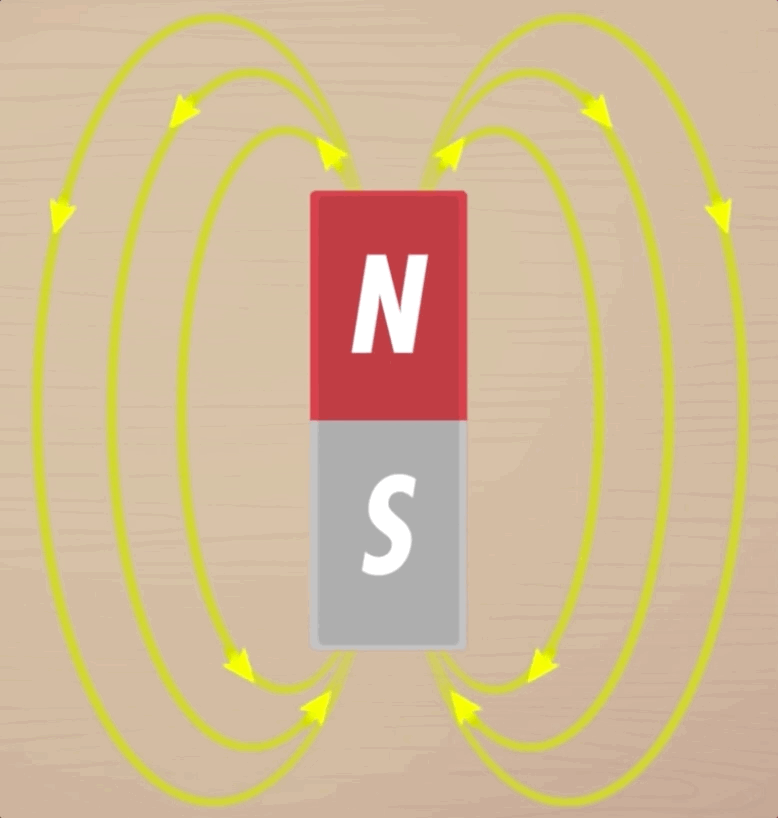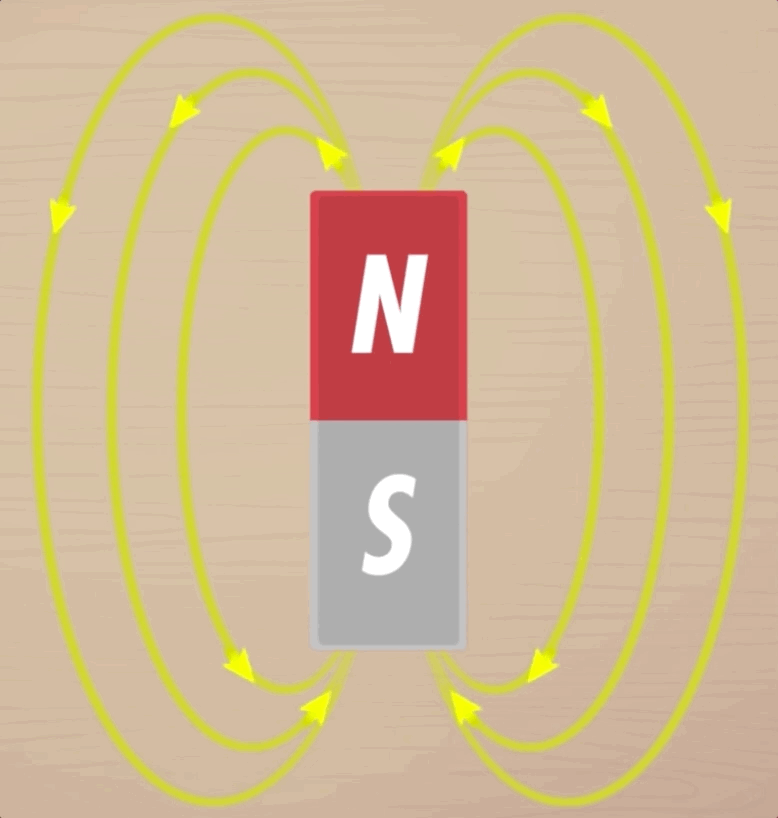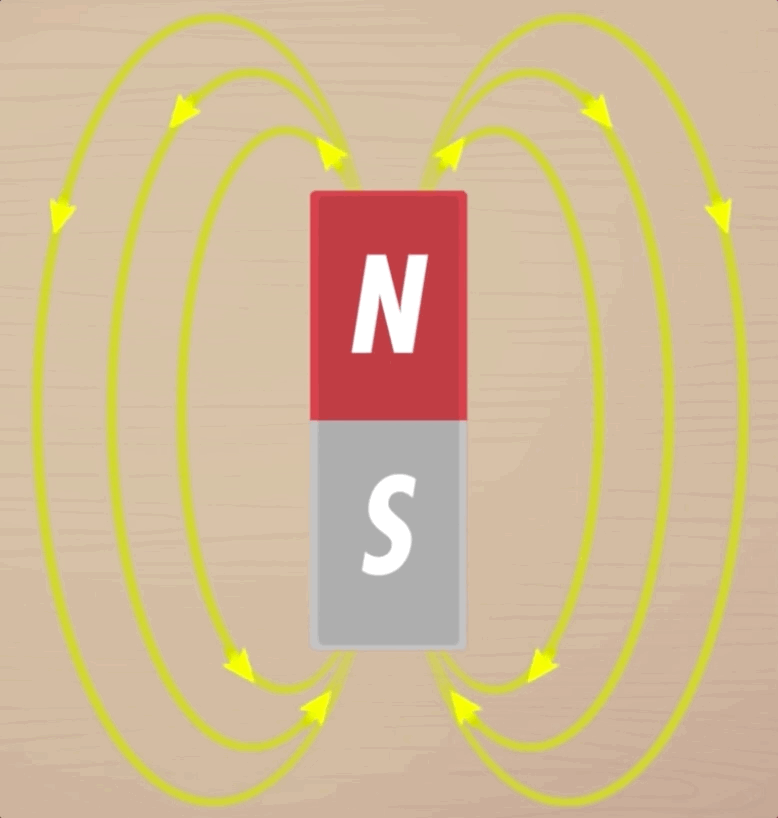
Uma característica bastante particular dos ímãs e que independe de sua forma, é a de que partindo o ímã ao meio, não conseguimos provocar a separação entre seus polos. Em outras palavras isso equivale a dizer que os polos de um ímã são indissociáveis de modo que essa propriedade estende-se inclusive aos limites atômicos do próprio material.

Magnetismo gerado por Corrente Elétrica
O Campo Magnético pode ser gerado de maneira digamos, artificial por meio de uma corrente elétrica. Foi o que descobriu no ano de 1819 o Físico Dinamarquês Hans Christian Øersted quando ao preparar-se para uma palestra percebeu que a agulha magnética de sua bússola sofria deflexão quando uma corrente elétrica passava por um fio posicionado próximo da agulha.

Após observado por Øersted que a agulha de uma bússola sofria uma deflexão quando era colocada próxima de um fio condutor percorrido por corrente elétrica, dois cientistas, Jean-Baptiste Biot (1774–1862) e Félix Savart (1791– 1841) realizaram experimentos quantitativos no sentido de caracterizar a força magnética sobre um ímã quando este era aproximado de um fio condutor percorrido por corrente elétrica.
Para calcularmos o valor do Campo Magnético gerado no espaço por um fio no qual percorre uma corrente elétrica, usaremos uma ferramenta matemática.
Vamos imaginar um fio condutor sendo percorrido por corrente elétrica, sendo que ao seu redor um campo magnético de forma circular e composto por linhas fechadas e concêntricas ao fio, se estabelece;ece no espaço. Algo que podemos visualizar na animação abaixo.
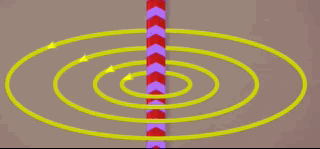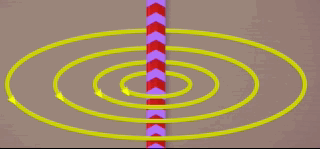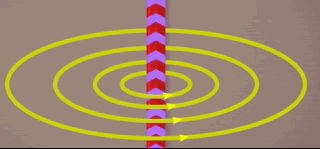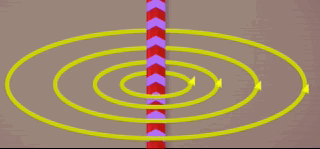
Ao redor desse fio, e com a mesma forma das linhas de campo escolheremos, uma circunferência cujo interior contenha as linhas de campo magnético.

Embora a linha de campo magnético tenha o formato circular, o campo magnético é uma grandeza vetorial, o que faz com que possamos atribuir a cada ponto da linha de campo magnético um vetor campo magnético.
Esse vetor tem a característica de ser tangente às linhas de campo magnético que se formam ao redor do fio.
Podemos dividir esse caminho circular em pequenos intervalos, sendo que para toda a circunferência, teremos para cada ponto dela, uma parte desse caminho e um vetor campo magnético associado a ele.

Para realizarmos essa operação de soma de todas essas contribuições. tomamos o produto desses dois vetores ao longo de toda a circunferência.
A operação matemática para a resolução desse problema é dada pela chamada Lei de Ampère, que constitui uma das equações fundamentais do eletromagnetismo.
Essa operação envolve matemática avançada, que fica apenas como sugestão de estudo. Seu resultado porém é importante e pode ser expresso em termos mais simples.
Que é a expressão para o campo magnético gerado ao redor de um fio de comprimento infinito.
Uma aplicação desse resultado é que nos possibilita calcular a intensidade de um campo magnético ao redor de um fio, quando percorrido por uma corrente.
