Para que possamos descrever um fenômeno físico, nós devemos estabelecer um sistema de referência. Conforme visto na página anterior, referenciais ditos inerciais são aqueles em que a primeira lei de Newton é verificada. Podemos estender esse conceito lembrando que todo referencial que se move com velocidade constante em relação a um referencial inercial, é também um referencial inercial.
Conforme discussão iniciada em Relatividade Galileana, gostaríamos de descrever o movimento de um corpo em diferentes referencias inerciais.
O princípio da relatividade Galileana diz que as leis da mecânica devem ser as mesmas em todos os referenciais inerciais. Isso posto, deve haver uma equivalência entre os sistemas de coordenadas existentes entre dois referenciais. Suponhamos que um fenômeno físico, que chamaremos de evento, ocorre e é observado por alguém em repouso num referencial inercial (por exemplo, uma luz piscando é um evento). Dizer que alguém encontra-se em repouso com relação a um referencial, quer dizer que sua posição não se altera nesse dado referencial.
O evento pode ser localizado e datado assim que utilizarmos as três coordenadas espaciais e uma coordenada temporal:
![]()
Devemos ser capazes portanto, de transformar essas coordenadas de um referencial no qual o observador encontra-se em repouso, em coordenadas de um observador em num referencial que se move com velocidade constante comparado ao primeiro (logo, também inercial).
Tomaremos dois referenciais inerciais que chamaremos de ![]() e
e ![]() . O referencial
. O referencial ![]() move-se com velocidade constante de módulo
move-se com velocidade constante de módulo ![]() ao longo da direção dos eixos
ao longo da direção dos eixos![]() e
e ![]() , paralelos entre si, sendo essa velocidade relativa ao sistema de referências
, paralelos entre si, sendo essa velocidade relativa ao sistema de referências ![]() . Assumiremos que as origens dos dois sistemas de referências coincidem quando a coordenada temporal for zero (
. Assumiremos que as origens dos dois sistemas de referências coincidem quando a coordenada temporal for zero (![]() ).
).
Vamos supor que um evento ![]() ocorra num dado ponto do espaço, num dado instante. Para simplificarmos, iremos imaginar nossos observadores localizados nas respectivas origens dos sistemas de coordenadas. Um observador
ocorra num dado ponto do espaço, num dado instante. Para simplificarmos, iremos imaginar nossos observadores localizados nas respectivas origens dos sistemas de coordenadas. Um observador ![]() na origem de
na origem de ![]() e um observador
e um observador ![]() na origem de
na origem de ![]() estão representados nos sistemas de referências como dois pontos vermelhos.
estão representados nos sistemas de referências como dois pontos vermelhos.
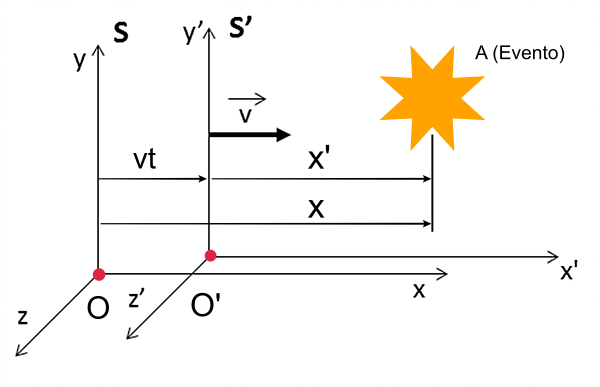 O evento tem coordenadas diferentes nos dois referenciais; no referencial
O evento tem coordenadas diferentes nos dois referenciais; no referencial ![]() temos
temos
![]()
enquanto que no referencial ![]() ,
,
![]()
Embora as coordenadas sejam diferentes, elas representam o mesmo evento.
Tratando a origem do referencial ![]() como se fosse uma partícula se deslocando para a direira com velocidade constante
como se fosse uma partícula se deslocando para a direira com velocidade constante ![]() relativa ao referencial
relativa ao referencial ![]() , podemos escrever as equações que relacionam os dois sistemas de coordenadas num instante de tempo
, podemos escrever as equações que relacionam os dois sistemas de coordenadas num instante de tempo ![]() . Pela figura acima,
. Pela figura acima,
(1) 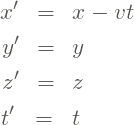
Essas são as equações de transformação espaço-temporais de Galileu. Note que o tempo é uma coordenada invariante nessas transformações, ou seja, ![]() , uma vez que o tempo para Galileu e para toda a mecânica de Newton é absoluto, ou seja, igual para todos os observadores.
, uma vez que o tempo para Galileu e para toda a mecânica de Newton é absoluto, ou seja, igual para todos os observadores.
Por conta da equivalência entre os dois referenciais, podemos escrever as equações de transformação a partir do referencial ![]() . As equações acima podem ser facilmente invertidas, produzindo
. As equações acima podem ser facilmente invertidas, produzindo
(2) 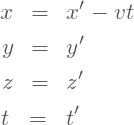
Implicações das Transformações de Galileu
Vamos agora discutir as implicações das transformações de Galileu. Os resultados que apresentamos abaixo são bastante familiares aos alunos do Ensino Médio. Afinal, nós temos a percepção da clássica (newtoniana) do mundo.
A invariância do tempo e do espaço
De acordo com o nosso senso comum, o tempo é uma grandeza absoluta, embora ele pareça passar mais devagar quando estamos fazendo uma coisa chata ou estamos entediados. Mas só parece, pois um intervalo de tempo marcado pelo seu relógio será exatamento o mesmo de um outro relógio qualquer, desde que ambos os relógios sejam similares.
Na mecânica newtoniana, o tempo é invariante – não importante em qual referencial ele seja medido. Todos medem o mesmo intervalo de tempo. As transformações de Galileu, por construção, já leva isso em conta, pois ![]() .
.
A distância percorrida também é invariante. Podemos fazer um percurso devagar ou rápido, mas a distância percorrida é sempre a mesma, para qualquer observador, em qualquer referencial.
Vamos supor que ![]() é um referencial que se encontra em repouso em relação a um trem, que por sua vez se move com velocidade
é um referencial que se encontra em repouso em relação a um trem, que por sua vez se move com velocidade ![]() constante na direção
constante na direção ![]() , para à direita, em relação a uma plataforma, onde o referencial
, para à direita, em relação a uma plataforma, onde o referencial ![]() se encontra em repouso.
se encontra em repouso.
Vamos medir o comprimento de uma barra em ambos os referenciais. Suponha que no trem haja uma barra deitada horizontalmente na direção ![]() . Por medida, entendemos que tenhamos dois eventos simultâneos num determinado referencial onde se queira fazer a medida. No caso, no referencial
. Por medida, entendemos que tenhamos dois eventos simultâneos num determinado referencial onde se queira fazer a medida. No caso, no referencial ![]() . O evento
. O evento ![]() ocorre numa extremidade da barra e o evento
ocorre numa extremidade da barra e o evento ![]() na outra. Da transformação de Galileu acima,
na outra. Da transformação de Galileu acima,
![]()
onde substituimos ![]() por
por ![]() sem qualquer problema, pois
sem qualquer problema, pois ![]() .
.
Lembrando que cada evento ocorre num determinado lugar, num determinado tempo, temos que para os eventos ![]() e
e ![]() ,
,
![]()
Lembrando que para realizar a medida, é preciso que os dois eventos ocorram simultaneamente naquele referencial que se quer fazer a medida, ![]() . Subtraindo a segunda da primeira,
. Subtraindo a segunda da primeira,
![]()
Mas ![]() é a diferença de posição dos eventos que ocorrem na extremidade da barra, portanto a diferença é o comprimento da barra (estamos assumindo aqui que
é a diferença de posição dos eventos que ocorrem na extremidade da barra, portanto a diferença é o comprimento da barra (estamos assumindo aqui que ![]() ), que denotaremos como sendo
), que denotaremos como sendo ![]() e o chamaremos de comprimento próprio, pois medido no referencial em que a barra estava em repouso.
e o chamaremos de comprimento próprio, pois medido no referencial em que a barra estava em repouso.
Por outro lado, ![]() é o comprimento da vara medida pelo referencial
é o comprimento da vara medida pelo referencial ![]() , que está em repouso, na plataforma. Logo,
, que está em repouso, na plataforma. Logo,
![]()
ou seja, ambos os referenciais medem um mesmo comprimento – resultado óbvio.
Transformações da velocidade
As equações (1) e (2) acima relacionam as coordenadas de posição de dois referenciais inerciais. Como a velocidade é a variação do espaço em relação ao tempo, podemos obter a relação entre as velocidades nessas coordenadas, utilizando uma delas.
Na linguagem do cálculo diferencial, a velocidade instantânea é a derivada temporal da posição. Logo,
(3) 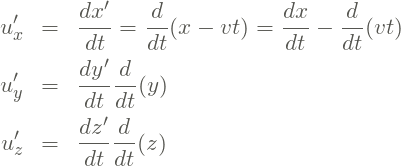
Como ![]() é constante (velocidade relativa entre os dois referenciais inerciais), conclui-se que
é constante (velocidade relativa entre os dois referenciais inerciais), conclui-se que
(4) 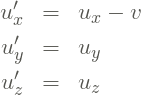
O resultado acima é familiar; tratam-se de componentes da velocidade relativa de um referencial que se move com velocidade ![]() na direção
na direção ![]() , em relação a outro.
, em relação a outro.
A equação (4) é a regra de transformação da velocidade na relatividade galileana, ou mecânica newtoniana.
Exemplo:
Vamos considerar que o referencial ![]() se encontrar num trem, que se move com velocidade uniforme
se encontrar num trem, que se move com velocidade uniforme ![]() na direção
na direção ![]() em relação à estação, onde se encontrar o referencial
em relação à estação, onde se encontrar o referencial ![]() .
.
Se do referencial do trem verificarmos que um objeto possui velocidade ![]() (está se movendo mais rápido que o teem, na mesma direção e sentido), alguém da estação vai concluiro que a velocidade do objeto é (de acordo com a primeira linha da equação (4)):
(está se movendo mais rápido que o teem, na mesma direção e sentido), alguém da estação vai concluiro que a velocidade do objeto é (de acordo com a primeira linha da equação (4)):
![]()
ou seja, mede uma velocidade maior: velocidade do objeto medida do trem mais a velocidade do trem.
Transformações da força
Para conseguirmos descrever completamente o movimento de um corpo em cada um dos referenciais, devemos conhecer a força nesses referenciais.
Para um corpo de massa ![]() constante, a força resultante é dada pela segunda lei de Newton,
constante, a força resultante é dada pela segunda lei de Newton, ![]() .
.
Se conhecermos a força no referencial ![]() , podemos obtê-la no referencial
, podemos obtê-la no referencial ![]() através da equação (3). Para isto, lembramos que a aceleração instantânea é a variação da velocidade por tempo, ou seja, é a derivada temporal da velocidade. Lembrando novamente qye
através da equação (3). Para isto, lembramos que a aceleração instantânea é a variação da velocidade por tempo, ou seja, é a derivada temporal da velocidade. Lembrando novamente qye ![]() é constante, obtemos
é constante, obtemos
![]()
ou seja, como as acelerações são iguais e as massas também,
![]()
O resultado é consistente com as conclusões de Galileu: a percepção do movimento é diferente porque as velocidades ![]() e
e ![]() do objeto são diferentes e portanto dependentes do referencial escolhido, mas a força resultante é a mesma. Independentemente do referencial, todos concluiriam que as leis físicas são invariantes.
do objeto são diferentes e portanto dependentes do referencial escolhido, mas a força resultante é a mesma. Independentemente do referencial, todos concluiriam que as leis físicas são invariantes.
Mas o que significa que as “leis físicas são invariantes”? Neste caso, estamos falando da invariância da força. Vamos supor, por exemplo, que existam duas partículas carregadas, de cargas ![]() e
e ![]() . Observadores em ambos os referenciais,
. Observadores em ambos os referenciais, ![]() e
e ![]() , concordam que a força que age sobre cada uma delas é dada pela lei de Coulomb:
, concordam que a força que age sobre cada uma delas é dada pela lei de Coulomb:
![Rendered by QuickLaTeX.com \[ |\vec{F}| = \frac{1}{4\pi\varepsilon_0}\frac{q_1q_2}{r^2} \]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-bddc88eea25224e54963cba6193ed872_l3.png)
onde ![]() é a separação entre as cargas.
é a separação entre as cargas.
Vamos analisar a seguir um processo de colisão entre duas partículas em ambos os referenciais e concluir que a força que haja entre elas é invariante.
Colisões
Num processo de colisão, podemos muitas vezes desprezar as forças externas que agem sobre o sistema de dois corpos, visto que as forças impulsivas, que atuam durante a colisão, geralmente são muito mais intensas que forças externas.
Como essas forças internas formam um par de forças do tipo ação e reação, vimos pela terceira lei de Newton que o momento linear do sistema se conserva:
![Rendered by QuickLaTeX.com \[ \vec{F}_\textrm{res} = 0 = \frac{d\vec{P}_\textrm{total}}{dt} = \frac{d}{dt}(\vec{p}_1 + \vec{p}_2) \quad \Rightarrow \quad \vec{p}_1 + \vec{p}_2 = \textrm{ constante} \]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-3074ed176e691e264a3c219dc5945596_l3.png)
Do nosso resultado da invariância da força, as forças de interação observadas são sempre as mesmas em qualquer referencial inercial do qual se observa tais colisões.
O que significa isto na prática? Os jogadores não irão notar diferença alguma se uma partida de bilhar ocorrer num vagão de um trem à velocidade constante ou se ocorrer no solo.
A seguir, vamos analisar a colisão unidimensional entre dois corpos em dois referencias inerciais distintos.
Por simplicidade, vamos tomar a colisão entre corpos de mesma massa ![]() kg, que se deslocam em sentido contrário com velocidades de mesma intensidade
kg, que se deslocam em sentido contrário com velocidades de mesma intensidade ![]() m/s, num referencial inercial
m/s, num referencial inercial ![]() . Aqui ficará convencionado que o corpo A movimenta-se inicialmente no sentido positivo do eixo
. Aqui ficará convencionado que o corpo A movimenta-se inicialmente no sentido positivo do eixo ![]() do sistema de referência adotado.
do sistema de referência adotado.
Se num determinado instante essas duas partículas colidem elasticamente por um intervalo de tempo de 1 ms, qual o valor da força de interação entre as duas partículas durante a colisão?
Assumindo que se trata de um sistema isolado, o momento linear do sistema deverá se conservar. Além do mais, a colisão é elástica, o que significa que o sistema também conserva sua energia cinética.
A força envolvida no processo dependerá do tempo de interação e da variação do momento linear. Na página Colisões, do site da professora Ivânia de Oliveira, contém uma estudo mais detalhado sobre colisões.
No site, é mostrado que numa colisão elástica unidimensional envolvendo partículas de mesma massa, as velocidades são trocadas. Logo, se as velocidades das partículas A e B antes da colisão forem, respectivamente,
![]()
as velocidades finais serão
![]()
A variação do momento linear da partícula A será
![]()
Portanto,
![]()
A variação do momento linear é igual à quantidade que chamamos de impulso, ![]() . Mas,
. Mas,
![Rendered by QuickLaTeX.com \[ \Delta p = J = \int F\: dt = F_\textrm{med} \Delta t \]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-80edeb6160efafc2465aa49747be5890_l3.png)
A integral é para indicar que ![]() é a área abaixo do gráfico da força versus tempo, até o eixo do tempo, no intervalo
é a área abaixo do gráfico da força versus tempo, até o eixo do tempo, no intervalo ![]() .
.
Temos que
![]()
O sinal negativo indica que a força sobre A é para à esquerda. Pode-se verificar que a força agindo sobre a outra partícula possui o mesmo módulo, mas sentido contrário, pois ambas constituem um par ação-reação.
A seguir, o problema será analisado do ponto de vista de um outro referencial. Vamos tomar um referencial que viaje junto, antes da colisão, com a partícula A. Esse referencial receberá o nome de ![]() . Como deverá ser a força atuando sobre as partículas durante a colisão, nesse referencial?
. Como deverá ser a força atuando sobre as partículas durante a colisão, nesse referencial?
Em relação ao referencial de solo ![]() ,
, ![]() se move com velocidade
se move com velocidade ![]() m/s. Temos que em
m/s. Temos que em ![]() a partícula A está em repouso. Logo,
a partícula A está em repouso. Logo, ![]() .
.
Já a partícula B terá, pela equação (4), velocidade inicial
![]()
Após a colisão, haverá novamente troca de velocidades, pois se trata de uma colisão unidimensional elástica entre corpos com mesma massa. Logo,
![]()
Observe que o referencial ![]() continua com velocidade
continua com velocidade ![]() . Como
. Como ![]() , agora a partícula B acompanha o referencial
, agora a partícula B acompanha o referencial ![]() .
.
Tomando novamente a expressão que permite calcular a força sobre as partículas, obtém-se para a partícula A
![Rendered by QuickLaTeX.com \[ F_\textrm{med}^\prime = \frac{\Delta p_A'}{\Delta t} = \frac{m_A u_{A,f}^\prime - m_A u_{A, i}^\prime}{\Delta t} \]](https://relatividade-restrita.propg.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-c12bb4a51eb53106771f170f2c54e0a9_l3.png)
Logo, substituindo os dados,
![]()
o que concluimos que a força sobre A não depende do referencial.
Esse resultado mostra a invariância das interações entre corpos observadas a partir de diferentes referenciais inerciais. De outra forma, as leis de Newton são invariantes por transformação de Galileu quando se passa de um referencial inercial ![]() para um outro
para um outro ![]() . Ambos são igualmente válidos para descrever um fenômeno físico.
. Ambos são igualmente válidos para descrever um fenômeno físico.
Mas será que todos os fenômenos físicos são consistentes com os resultados que obtivemos aqui?
Vamos mostrar que “coisas estranhas” começaram a ser observadas/discutidas na virada do Séc. XIX para o XX, apontando que a chamada Mecânica Newtoniana, que são consistentes com as transformações de Galileu, começa a falhar.
